题目内容
20.解方程组$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$时,一学生把c看错而得$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$,而正确的解是$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$,那么a-b-c=1.分析 把错误解与正确解分别代入方程组中第一个方程,求出a与b的值,将正确解代入方程组第二个方程求出c的值,即可求出a-b-c的值.
解答 解:把$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$与$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$分别代入ax+by=2中得:$\left\{\begin{array}{l}{-2a+2b=2①}\\{3a-2b=2②}\end{array}\right.$,
①+②得:a=4,
把a=4代入①得:b=5,
把$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$代入cx-7y=8中得:3c+14=8,即c=-2,
则a-b-c=4-5+2=1.
故答案为:1
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.关于x的方程(m-3)x${\;}^{{m}^{2}-2m-1}$-mx+6=0是一元二次方程,则它的一次项系数是( )
| A. | -1 | B. | 1 | C. | 3 | D. | 3或-1 |
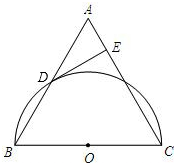 已知△ABC是等边三角形,以BC为直径的半圆O与边AB相交于点D,DE⊥AC,垂足为点E.
已知△ABC是等边三角形,以BC为直径的半圆O与边AB相交于点D,DE⊥AC,垂足为点E.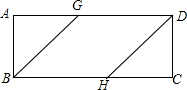 在矩形ABCD中,AB=1,BG、DH分别平分∠ABC、∠ADC,交AD、BC于点G、H.要使四边形BHDG为菱形,则AD的长为1+$\sqrt{2}$.
在矩形ABCD中,AB=1,BG、DH分别平分∠ABC、∠ADC,交AD、BC于点G、H.要使四边形BHDG为菱形,则AD的长为1+$\sqrt{2}$.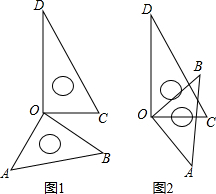 (1)如图1所示,将一副三角尺的直角顶点重合在点O处.
(1)如图1所示,将一副三角尺的直角顶点重合在点O处.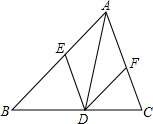 已知,如图所示,△ABC中,AD是角平分线,E、F分别是AB、AC上的点,且DE∥AC,DF∥AB,试说明四边形ABDF是菱形.
已知,如图所示,△ABC中,AD是角平分线,E、F分别是AB、AC上的点,且DE∥AC,DF∥AB,试说明四边形ABDF是菱形.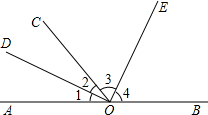 如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.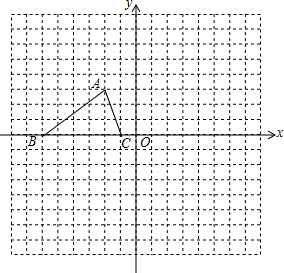 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).将△ABC绕坐标原点O逆时针旋转90°,得到△A′B′C′,画出△A′B′C′.并计算点A旋转经过的路径长度.
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).将△ABC绕坐标原点O逆时针旋转90°,得到△A′B′C′,画出△A′B′C′.并计算点A旋转经过的路径长度.