题目内容
9．
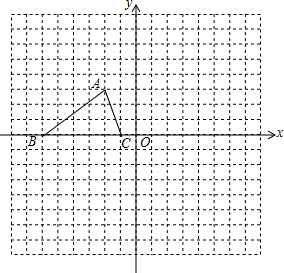如图，已知△ABC的三个顶点的坐标分别为A（-2，3）、B（-6，0）、C（-1，0）．将△ABC绕坐标原点O逆时针旋转90°，得到△A′B′C′，画出△A′B′C′．并计算点A旋转经过的路径长度．
分析 利用网格特点和旋转的性质画出点A、B、C的对应点A′、B′、C′，从而得到△A′B′C′，由于点A旋转经过的路径是以点O为圆心，OA为半径，圆心角为90°的弧，所以利用弧长公式可计算出点A旋转经过的路径长度．
解答 解：如图，△A′B′C′为所作；
OA=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$，
所以A旋转经过的路径长度=$\frac{90•π•\sqrt{13}}{180}$=$\frac{\sqrt{13}}{2}$π．
点评 本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
19．下列方程中，是一元一次方程的是（ ）
| A． | x2-4x=3 | B． | $\frac{y}{2}$+2y=3 | C． | x+2y=1 | D． | x-1=$\frac{1}{x}$ |
17．二次函数y=3x2的图象向右平移一个单位后函数解析式为（ ）
| A． | y=3x2+1 | B． | y=3x2-1 | C． | y=3（x-1）2 | D． | y=3（x+1）2 |
4．将下列多项式分解因式，结果中不含因式x+1的是（ ）
| A． | x2-1 | B． | x2-2x+1 | C． | x（x-2）+（x-2） | D． | x2+2x+1 |
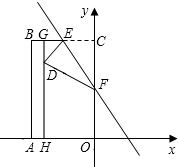如图，矩形OABC在平面直角坐标系内（O为坐标原点），点A在x轴上，点C在y轴上，点B的坐标为（-4，6），点E是BC的中点，点H在OA上，且AH=1，过点H且平行于y轴的HG与EB交于点G，现将矩形折叠，使顶点C落在HG上，并与HG上的点D重合，折痕为EF，点F为折痕与y轴的交点．CF=2$\sqrt{3}$．
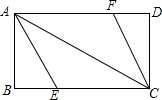同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形，他沿矩形的对角线AC折出∠CAE=∠DAC，∠ACF=∠ACB的方法得到四边形AECF（如图）．
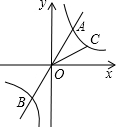如图．过原点O的直线y=k1x和y=k2x与反比例$\frac{1}{x}$（x＞0）的象分别交于点A、C．