题目内容
17.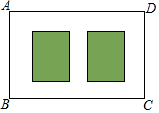 要对一块长90米,宽40米的矩形荒地ABCD进行绿化和硬化,设计方案如图所示,矩形P,Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽度都相等,并使两块绿地面积的和为矩形ABCD面积的$\frac{1}{3}$,求P、Q两块绿地周围的硬化路面的宽.
要对一块长90米,宽40米的矩形荒地ABCD进行绿化和硬化,设计方案如图所示,矩形P,Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽度都相等,并使两块绿地面积的和为矩形ABCD面积的$\frac{1}{3}$,求P、Q两块绿地周围的硬化路面的宽.
分析 可把P,Q通过平移看做一个矩形,设P、Q两块绿地周围的硬化路面的宽都为x米,用含x的代数式分别表示出绿地的长为(90-3x)米,宽为(40-2x)米,利用“两块绿地面积的和为矩形ABCD面积的$\frac{1}{3}$”作为相等关系列方程求解即可.
解答 解:设P、Q两块绿地周围的硬化路面的宽都为x米,根据题意,得
(90-3x)(40-2x)=90×40×$\frac{1}{3}$,
解得:x1=10,x2=40,
经检验,x2=40不符合题意,舍去.
答:两块绿地周围的硬化路面宽都为10米.
点评 考查了一元二次方程的应用,解题的关键是通过平移的方法,把分开的两块绿地合成一块长方形的绿地,利用其面积是矩形ABCD面积的$\frac{1}{3}$作为相等关系列方程.

练习册系列答案
相关题目
8.为了筹款支持希望工程,某“爱心”小组决定利用暑假销售一批进价为10元的小商品,为寻求合适的销售价格,他们进行了4天的试销,试销情况如表:
(1)猜测并确定y与x之间的一个函数关系式;
(2)若该小组计划每天的销售利润为450元,则其单价应为多少元?
| 第1天 | 第2天 | 第3天 | 第4天 | |
| 日销售单价x(元) | 20 | 30 | 40 | 50 |
| 日销售量y(个) | 30 | 20 | 15 | 12 |
(2)若该小组计划每天的销售利润为450元,则其单价应为多少元?
6.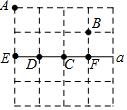 如图的4×4的正方形网格中,有A、B两点,在直线a上求一点P,使PA+PB最短,则点P应选在( )
如图的4×4的正方形网格中,有A、B两点,在直线a上求一点P,使PA+PB最短,则点P应选在( )
 如图的4×4的正方形网格中,有A、B两点,在直线a上求一点P,使PA+PB最短,则点P应选在( )
如图的4×4的正方形网格中,有A、B两点,在直线a上求一点P,使PA+PB最短,则点P应选在( )| A. | C点 | B. | D点 | C. | E点 | D. | F点 |
8.已知关于的方程3x-2m+1=0与2-m=2x的解互为相反数,则m=( )
| A. | -$\frac{8}{7}$ | B. | -4 | C. | -3 | D. | $\frac{8}{7}$ |
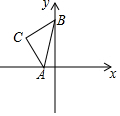 如图,在平面直角坐标系中,△ABC是以C为直角顶点的直角三角形,且AC=BC,点A的坐标为(-1,0),点B的坐标为(0,4),则点C的坐标为(-$\frac{5}{2}$,$\frac{5}{2}$).
如图,在平面直角坐标系中,△ABC是以C为直角顶点的直角三角形,且AC=BC,点A的坐标为(-1,0),点B的坐标为(0,4),则点C的坐标为(-$\frac{5}{2}$,$\frac{5}{2}$).