题目内容
如图，在矩形ABCD中，AB=12cm，BC=6cm，点E、F分别在AB、CD上，将矩形ABCD沿EF折叠，使点A、D分别落在矩形ABCD外部的点A1、D1处，则整个阴影部分图形的周长为（ ）| A、72cm | B、18cm |
| C、40cm | D、36cm |
考点：翻折变换（折叠问题）
专题：
分析：根据折叠的性质，得A1E=AE，A1D1=AD，D1F=DF，则阴影部分的周长即为矩形的周长．
解答：解：根据折叠的性质，得
A1E=AE，A1D1=AD，D1F=DF．
则阴影部分的周长=矩形的周长=2（12+6）=36（cm）．
故选：D．
A1E=AE，A1D1=AD，D1F=DF．
则阴影部分的周长=矩形的周长=2（12+6）=36（cm）．
故选：D．
点评：此题要能够根据折叠的性质得到对应的线段相等，从而求得阴影部分的周长．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
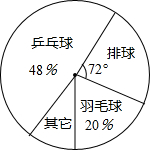某班60名学生喜欢各类体育活动，他们最喜欢的一项体育活动情况见扇形统计图，现给出以下说法①最受欢迎的球类运动是乒乓球；
②最喜欢排球的学生达到班级学生总数的
| 1 |
| 5 |
③最喜欢羽毛球的学生达到班级学生总数的12人．
④最喜欢其他运动的学生达到12%
其中正确的结论为（ ）
| A、①②③ | B、①③④ |
| C、①②④ | D、①②③④ |
已知关于x的不等式
有四个整数解，则a的取值范围是（ ）
|
| A、10＜a＜11 |
| B、10≤a＜11 |
| C、10＜a≤11 |
| D、10≤a≤11 |
若x+m与x+
乘积的值不含x项，则m的值为（ ）
| 1 |
| 4 |
A、
| ||
| B、4 | ||
C、-
| ||
| D、-4 |
下列图形∠1与∠2互为顶角的是（ ）
A、 |
B、 |
C、 |
D、 |
在四边形中，能判定这个四边形是正方形的条件是（ ）
| A、对角线相等，对边平行且相等 |
| B、一组对边平行，一组对角相等 |
| C、对角线互相平分且相等，对角线互相垂直 |
| D、一组邻边相等，对角线互相平分 |
反比例函数y=-
与正比例函数y=kx的一个交点为（-1，2），则关于x的方程-
=kx的解为（ ）
| 2 |
| x |
| 2 |
| x |
| A、x1=-1，x2=1 |
| B、x1=-1，x2=2 |
| C、x1=-2，x2=1 |
| D、x1=-1，x2=-2 |