题目内容
7.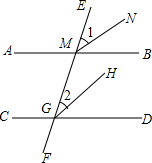 如图,直线AB∥CD,EF分别交AB、CD于点M、G,MN平分∠EMB,GH平分∠MGD,求证:MN∥GH.
如图,直线AB∥CD,EF分别交AB、CD于点M、G,MN平分∠EMB,GH平分∠MGD,求证:MN∥GH.证明:∵AB∥CD已知
∴∠EMB=∠EGD两直线平行,同位角相等
∵MN平分∠EMB,GH平分∠MGD(已知)
∴∠1=$\frac{1}{2}$∠EMB,∠2=$\frac{1}{2}$∠MGD角平分线的定义
∴∠1=∠2
∴MN∥GH同位角相等,两直线平行.
分析 由平行线的性质可求得∠EMB=∠EGD,再由角平分线的定义可得∠1=∠2,可证明MN∥GH,据此填空即可.
解答 证明:∵AB∥CD 已知,
∴∠EMB=∠EGD 两直线平行,同位角相等,
∵MN平分∠EMB,GH平分∠MGD(已知)
∴∠1=$\frac{1}{2}$∠EMB,∠2=$\frac{1}{2}$∠MGD 角平分线的定义,
∴∠1=∠2,
∴MN∥GH 同位角相等,两直线平行.
故答案为:已知;两直线平行,同位角相等;角平分线的定义;∠1=∠2;同位角相等,两直线平行.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
17.下列各式成立的是( )
| A. | $\sqrt{(-3)^{2}}$=-3 | B. | $\sqrt{4+9}$=$\sqrt{4}$+$\sqrt{9}$ | C. | $\sqrt{3×9}$=$\sqrt{3}$×$\sqrt{9}$ | D. | $\sqrt{{x}^{2}}$=x |
 将自然数按如下的顺序排列.在这样的排列下,9排在第3行第2列,那么:
将自然数按如下的顺序排列.在这样的排列下,9排在第3行第2列,那么: