题目内容
3.(1)解分式方程:$\frac{x}{x-2}$-1=$\frac{6}{x+2}$;(2)化简求值:$\frac{a-b}{a}$÷(a-$\frac{2ab-{b}^{2}}{a}$),其中a=$\sqrt{2}$,b=$\sqrt{3}$.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)去分母得:x2+2x-x2+4=6x-12,
移项合并得:4x=16,
解得:x=4,
经检验x=4是分式方程的解;
(2)原式=$\frac{a-b}{a}$÷$\frac{{a}^{2}-2ab+{b}^{2}}{a}$=$\frac{a-b}{a}$•$\frac{a}{(a-b)^{2}}$=$\frac{1}{a-b}$,
当a=$\sqrt{2}$,b=$\sqrt{3}$时,原式=$\frac{1}{\sqrt{2}-\sqrt{3}}$=-$\sqrt{2}$-$\sqrt{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
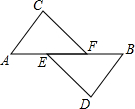 已知,AE=BF,AC∥DB,AC=DB,证明:CF=DE.
已知,AE=BF,AC∥DB,AC=DB,证明:CF=DE.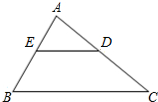 如图,D、E分别是AC、AB上的点,∠ADE=40°,∠C=40°,∠A=60°.
如图,D、E分别是AC、AB上的点,∠ADE=40°,∠C=40°,∠A=60°. 如图,四边形ABCD,∠A=∠D,∠ABC=∠BCD,∠1=∠2,∠4=∠5,写出图中平行关系,并证明.(提示:三角形内角和为180°)
如图,四边形ABCD,∠A=∠D,∠ABC=∠BCD,∠1=∠2,∠4=∠5,写出图中平行关系,并证明.(提示:三角形内角和为180°) 将自然数按如下的顺序排列.在这样的排列下,9排在第3行第2列,那么:
将自然数按如下的顺序排列.在这样的排列下,9排在第3行第2列,那么: