题目内容
7.已知函数y=ax2-4bx+3,(1)求证:无论a、b为何值,函数图象经过y轴上一个定点;
(2)当a、b满足什么条件时,图象与直线y=1有交点;
(3)若-1<x<0,a=1,当函数值y恒大于1时,求b的取值范围.
分析 (1)与y轴的交点坐标,也就是当x=0时,求得y值,得出交点坐标即可;
(2)图象与直线y=1有交点,也就是两个函数建立的方程有实数根,利用根的判别式解答即可;
(3)把x=-1,x=0,a=1分别代入函数解析式,由函数值y恒大于1建立不等式组求得b的取值范围即可.
解答 证明:(1)∵当x=0时,y=ax2-4bx+3=3,
∴函数图象与y轴的交点坐标为(0,3),
∴论a、b为何值,函数图象经过y轴上一个定点(0,3);
解:(2)∵象与直线y=1有交点,
∴1=ax2-4bx+3,
ax2-4bx+2=0,
∴△=(-4b)2-8a≥0,
解得:a≤2b2.
(3)∵-1<x<0,a=1,函数值y恒大于1,
∴1+4b>1,
解得:b>0.
点评 此题考查二次函数的性质,掌握二次函数与一次函数的交点问题是解决问题的关键.

练习册系列答案
相关题目
17.用-x表示的数一定是( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 无法确定 |
19.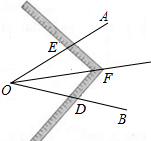 工人师傅经常利用角尺平分一个任意角,如图所示,∠AOB是一个任意角,在边OA,OB上分别取OD=OE,移动角尺,使角尺两边相同的刻度分别与D,E重合,这时过角尺顶点P的射线OP就是∠AOB的平分线.你认为工人师傅在此过程中用到的三角形全等的判定方法是这种作法的道理是( )
工人师傅经常利用角尺平分一个任意角,如图所示,∠AOB是一个任意角,在边OA,OB上分别取OD=OE,移动角尺,使角尺两边相同的刻度分别与D,E重合,这时过角尺顶点P的射线OP就是∠AOB的平分线.你认为工人师傅在此过程中用到的三角形全等的判定方法是这种作法的道理是( )
 工人师傅经常利用角尺平分一个任意角,如图所示,∠AOB是一个任意角,在边OA,OB上分别取OD=OE,移动角尺,使角尺两边相同的刻度分别与D,E重合,这时过角尺顶点P的射线OP就是∠AOB的平分线.你认为工人师傅在此过程中用到的三角形全等的判定方法是这种作法的道理是( )
工人师傅经常利用角尺平分一个任意角,如图所示,∠AOB是一个任意角,在边OA,OB上分别取OD=OE,移动角尺,使角尺两边相同的刻度分别与D,E重合,这时过角尺顶点P的射线OP就是∠AOB的平分线.你认为工人师傅在此过程中用到的三角形全等的判定方法是这种作法的道理是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
16.设方程x2-x-3=0的两根为x1,x2,则下列结论正确的是( )
| A. | x1x2=1 | B. | x1+x2=-3 | C. | x1+x2=1 | D. | x1x2=3 |
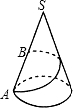 已知圆锥底面半径r=10cm,母线SA长为40cm.一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是20$\sqrt{5}$cm.
已知圆锥底面半径r=10cm,母线SA长为40cm.一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是20$\sqrt{5}$cm.