题目内容
2.已知:在平面直角坐标系中,点A(3a+2b,4a+b)在第四象限,且到x轴的距离为2,到y轴的距离为1.(1)求点B(2a+3b,2a+b)的坐标;
(2)若点C与点A关于x轴对称,请直接写出点C的坐标;
(3)在y轴上是否存在一点M,使△ACM的面积=$\frac{1}{2}$△ABC的面积?若存在,请求出点M的坐标;若不存在,请说明理由.
分析 首先由点A(3a+2b,4a+b)在第四象限,且到x轴的距离为2,到y轴的距离为1,得出建立方程组求得a、b;
(1)代入求得点B坐标;
(2)根据关于x轴对称点的坐标,横坐标相同,纵坐标互为相反数得出点C坐标;
(3)计算三角形的面积判定即可.
解答 解:∵点A(3a+2b,4a+b)在第四象限,且到x轴的距离为2,到y轴的距离为1,A为(1,-2),
∴$\left\{\begin{array}{l}{3a+2b=1}\\{4a+b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
(1)2a+3b=4,2a+b=0,点B为(4,0);
(2)C(1,2)
(3)不存在.理由:
由题意得:∵△ACM的面积=$\frac{1}{2}$×4×1=2,
△ABC的面积=$\frac{1}{2}$×4×3=6,
∴△ACM的面积=$\frac{1}{3}$△ABC的面积,
∴不存在点M.
点评 此题考查点的坐标与图形的性质,掌握点在平面直角坐标系中的性质是解决问题的关键.

练习册系列答案
相关题目
12.下列因式分解错误的是( )
| A. | x2+2xy-y2=(x-y)2 | B. | m2-4n2=(m+2n)(m-2n) | ||
| C. | x3y2-x5=x3(y-x)(y+x) | D. | x4-y4=(x+y)(x-y)(x2+y2) |
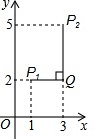 在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义: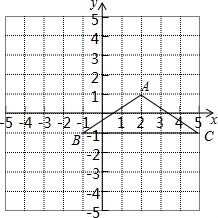 三角形ABC在平面直角坐标系中的位置如图所示.
三角形ABC在平面直角坐标系中的位置如图所示.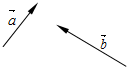 如图,已知两个不平行的向量$\overrightarrow{a}$、$\overrightarrow{b}$.先化简,再求作:(4$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$)-2($\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$)(不要求写作法,但要指出图中表示结论的向量)
如图,已知两个不平行的向量$\overrightarrow{a}$、$\overrightarrow{b}$.先化简,再求作:(4$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$)-2($\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$)(不要求写作法,但要指出图中表示结论的向量)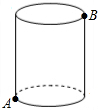 如图,有一圆柱,其高为8cm,它的底面半径为2cm,在圆柱下底面A处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离为2$\sqrt{17}$ cm.(π取3)
如图,有一圆柱,其高为8cm,它的底面半径为2cm,在圆柱下底面A处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离为2$\sqrt{17}$ cm.(π取3)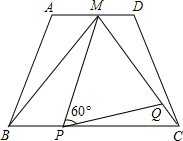 如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.
如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.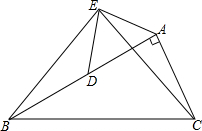 如图,在Rt△ABC中,∠BAC=90°,AB=2AC,点D是AB的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合(与Rt△ABC在同一平面内),连接BE,EC.试猜想线段BE和EC的数量及位置关系,并对你的猜想说明理由.
如图,在Rt△ABC中,∠BAC=90°,AB=2AC,点D是AB的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合(与Rt△ABC在同一平面内),连接BE,EC.试猜想线段BE和EC的数量及位置关系,并对你的猜想说明理由.