题目内容
12.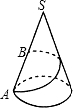 已知圆锥底面半径r=10cm,母线SA长为40cm.一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是20$\sqrt{5}$cm.
已知圆锥底面半径r=10cm,母线SA长为40cm.一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是20$\sqrt{5}$cm.
分析 最短路线应放在平面内,构造直角三角形,求两点之间的线段的长度.
解答  解:如图,由圆锥的侧面展开图可见,甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B所走的最短路线是线段AB的长.
解:如图,由圆锥的侧面展开图可见,甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B所走的最短路线是线段AB的长.
在Rt△ASB中,
∵SA=40,SB=20,
∴AB=20$\sqrt{5}$(cm).
∴甲虫走的最短路线的长度是20$\sqrt{5}$cm.
故答案为:20$\sqrt{5}$cm.
点评 本题考查的是平面展开-最短路径问题,根据题意画出圆锥的侧面展开图,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
3.某民政局决定向某灾区调运救灾帐篷1100顶,棉被1500床,切实保障好受灾群众基本生活.某运输车队义务承担了这次运输任务,一次性正好(即所用货车恰好全部装满)将救灾物资运往灾区,甲、乙两种货车一次可以运走两种救灾物资的数量如下表所示:
(1)需要甲、乙两种货车各多少辆?
(2)已知甲种货车每辆需运费1000元,乙种货车每辆运费1200元,则运费共多少元?
| 物资类型 汽车类型 | 帐篷 | 棉被 |
| 甲车 | 65 | 180 |
| 乙车 | 140 | 130 |
(2)已知甲种货车每辆需运费1000元,乙种货车每辆运费1200元,则运费共多少元?
17.下列计算正确的是( )
| A. | a3•a2=a6 | B. | (-a4)2=a6 | C. | -(ab)2=a2b2 | D. | a10÷a9=a |
4.如果x+y=1,x2+y2=3,那么x2-xy+y2的值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
1.在梯形ABCD中,AD∥BC,EF为梯形中位线,若AD=6,BC=10,则EF长是( )
| A. | 4 | B. | 2 | C. | 8 | D. | 6 |