题目内容
6.已知x=2-$\sqrt{3}$,y=2+$\sqrt{3}$,则($\frac{x+2\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}$+$\frac{1}{\sqrt{x}-\sqrt{y}}$)÷$\frac{x-y+1}{\sqrt{x}}$的值是$\frac{3-\sqrt{3}}{6}$.分析 先依据二次根式运算法则和性质化简原式,再将x、y的值代入计算可得.
解答 解:原式=($\sqrt{x}+\sqrt{y}$+$\frac{1}{\sqrt{x}-\sqrt{y}}$)•$\frac{\sqrt{x}}{x-y+1}$
=($\frac{x-y}{\sqrt{x}-\sqrt{y}}$+$\frac{1}{\sqrt{x}-\sqrt{y}}$)•$\frac{\sqrt{x}}{x-y+1}$
=$\frac{x-y-1}{\sqrt{x}-\sqrt{y}}$•$\frac{\sqrt{x}}{x-y+1}$
=$\frac{\sqrt{x}}{\sqrt{x}-\sqrt{y}}$
=$\frac{x+\sqrt{xy}}{x-y}$,
当x=2-$\sqrt{3}$,y=2+$\sqrt{3}$时,
原式=$\frac{2-\sqrt{3}+\sqrt{(2-\sqrt{3})(2+\sqrt{3})}}{2-\sqrt{3}-(2+\sqrt{3})}$
=$\frac{2-\sqrt{3}+1}{-2\sqrt{3}}$
=$\frac{3-\sqrt{3}}{6}$.
故答案为:$\frac{3-\sqrt{3}}{6}$.
点评 本题主要考查二次根式的化简与求值,熟练掌握二次根式的运算法则和性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
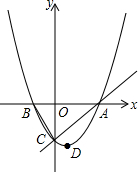 如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A,B两点,与y轴交于C点,A点的坐标为(4,0),P点是抛物线上的一个动点,且横坐标为m.
如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A,B两点,与y轴交于C点,A点的坐标为(4,0),P点是抛物线上的一个动点,且横坐标为m.