题目内容
5.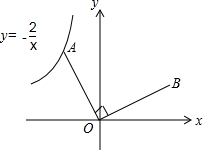 如图,已知点A是反比例函数y=-$\frac{2}{x}$的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为y=$\frac{2}{x}$.
如图,已知点A是反比例函数y=-$\frac{2}{x}$的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为y=$\frac{2}{x}$.
分析 设A(m,n),过A作AC⊥x轴于C,过B作BD⊥x轴于D,得到AC=n,OC=-m,根据全等三角形的性质得到AC=OD=n,CO=BD=-m,于是得到结论.
解答 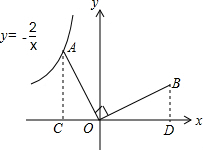 解:∵点A是反比例函数y=-$\frac{2}{x}$的图象上的一个动点,
解:∵点A是反比例函数y=-$\frac{2}{x}$的图象上的一个动点,
设A(m,n),
过A作AC⊥x轴于C,过B作BD⊥x轴于D,
∴AC=n,OC=-m,
∴∠ACO=∠BDO=90°,
∵∠AOB=90°,
∴∠CAO+∠AOC=∠AOC+∠BOD=90°,
∴∠CAO=∠BOD,
在△ACO与△ODB中$\left\{\begin{array}{l}{∠ACO=∠ODB}\\{∠CAO=∠BOD}\\{AO=BO}\end{array}\right.$,
∴△ACO≌△ODB,
∴AC=OD=n,CO=BD=-m,
∴B(n,-m),
∵mn=-2,
∴n(-m)=2,
∴点B所在图象的函数表达式为y=$\frac{2}{x}$,
故答案为:y=$\frac{2}{x}$.
点评 本题考查了坐标与图形变化-旋转,反比例函数图形上点的坐标特征,待定系数法求反比例函数的解析式,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
13.2016年某市用于资助贫困学生的助学金总额是9680000元,将9680000用科学记数法表示为( )
| A. | 96.8×105 | B. | 9.68×106 | C. | 9.68×107 | D. | 0.968×108 |
10.为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
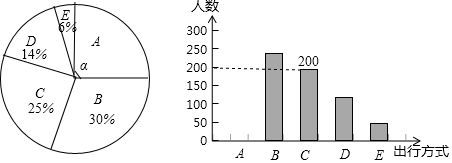
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有800人,其中选择B类的人数有240人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
| 种类 | A | B | C | D | E |
| 出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有800人,其中选择B类的人数有240人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
14.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
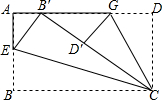 如图,将一张矩形纸片ABCD的边BC斜着向AD边对折,使点B落在AD上,记为B′,折痕为CE;再将CD边斜向下对折,使点D落在B′C边上,记为D′,折痕为CG,B′D′=2,BE=$\frac{1}{3}$BC.则矩形纸片ABCD的面积为15.
如图,将一张矩形纸片ABCD的边BC斜着向AD边对折,使点B落在AD上,记为B′,折痕为CE;再将CD边斜向下对折,使点D落在B′C边上,记为D′,折痕为CG,B′D′=2,BE=$\frac{1}{3}$BC.则矩形纸片ABCD的面积为15.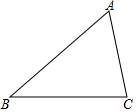 如图,△ABC中,∠ACB>∠ABC.
如图,△ABC中,∠ACB>∠ABC.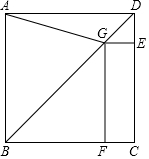 如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.