题目内容
16.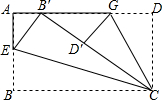 如图,将一张矩形纸片ABCD的边BC斜着向AD边对折,使点B落在AD上,记为B′,折痕为CE;再将CD边斜向下对折,使点D落在B′C边上,记为D′,折痕为CG,B′D′=2,BE=$\frac{1}{3}$BC.则矩形纸片ABCD的面积为15.
如图,将一张矩形纸片ABCD的边BC斜着向AD边对折,使点B落在AD上,记为B′,折痕为CE;再将CD边斜向下对折,使点D落在B′C边上,记为D′,折痕为CG,B′D′=2,BE=$\frac{1}{3}$BC.则矩形纸片ABCD的面积为15.
分析 根据翻折变化的性质和勾股定理可以求得BC和AB的长,然后根据矩形的面积公式即可解答本题.
解答 解:设BE=a,则BC=3a,
由题意可得,
CB=CB′,CD=CD′,BE=B′E=a,
∵B′D′=2,
∴CD′=3a-2,
∴CD=3a-2,
∴AE=3a-2-a=2a-2,
∴DB′=$\sqrt{CB{′}^{2}-C{D}^{2}}=\sqrt{(3a)^{2}-(3a-2)^{2}}$=$\sqrt{12a-4}$=2$\sqrt{3a-1}$,
∴AB′=3a-2$\sqrt{3a-1}$,
∵AB′2+AE2=B′E2,
∴$(3a-2\sqrt{3a-1})^{2}+(2a-2)^{2}={a}^{2}$,
解得,a=$\frac{2}{3}$或a=$\frac{5}{3}$,
当a=$\frac{2}{3}$时,BC=2,
∵B′D′=2,CB=CB′,
∴a=$\frac{2}{3}$时不符合题意,舍去;
当a=$\frac{5}{3}$时,BC=5,AB=CD=3a-2=3,
∴矩形纸片ABCD的面积为:5×3=15,
故答案为:15.
点评 本题考查翻折变化、矩形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用翻折的性质和矩形的面积公式解答.

练习册系列答案
相关题目
4.下列一元二次方程没有实数根的是( )
| A. | x2-2x=0 | B. | x2-1=0 | C. | x2+x+1=0 | D. | x2+2x+1=0 |
1.慈溪,因治南有溪而得名,慈溪的常住人口约为1460000人,1460000用科学记数法表示为( )
| A. | 0.146×107 | B. | 1.46×105 | C. | 14.6×105 | D. | 1.46×106 |
8. 如图所示的几何体的俯视图为( )
如图所示的几何体的俯视图为( )
 如图所示的几何体的俯视图为( )
如图所示的几何体的俯视图为( )| A. |  | B. |  | C. |  | D. |  |
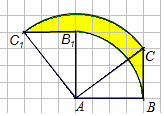 如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1,若网格小正方形的边长为1cm,则线段BC所扫过的图形(阴影部分)的面积为$\frac{9π}{4}$(结果保留π).
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1,若网格小正方形的边长为1cm,则线段BC所扫过的图形(阴影部分)的面积为$\frac{9π}{4}$(结果保留π). 如图,在△ABC中,∠C=75°,将△ABC绕点A顺时针旋转到△ADE的位置,点E恰好落在边BC上,且AD∥BC,则∠D的度数为30°.
如图,在△ABC中,∠C=75°,将△ABC绕点A顺时针旋转到△ADE的位置,点E恰好落在边BC上,且AD∥BC,则∠D的度数为30°.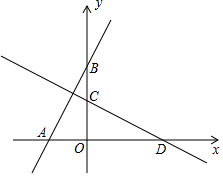 如图,在平面直角坐标系xOy中,过点A(-2,0)的直线交y轴正半轴于点B,将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D、C.
如图,在平面直角坐标系xOy中,过点A(-2,0)的直线交y轴正半轴于点B,将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D、C.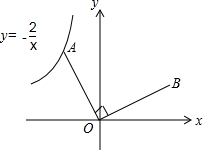 如图,已知点A是反比例函数y=-$\frac{2}{x}$的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为y=$\frac{2}{x}$.
如图,已知点A是反比例函数y=-$\frac{2}{x}$的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为y=$\frac{2}{x}$.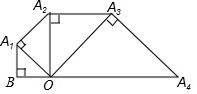 如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为($\sqrt{2}$)n.
如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为($\sqrt{2}$)n.