题目内容
20.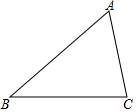 如图,△ABC中,∠ACB>∠ABC.
如图,△ABC中,∠ACB>∠ABC.(1)用直尺和圆规在∠ACB的内部作射线CM,使∠ACM=∠ABC(不要求写作法,保留作图痕迹);
(2)若(1)中的射线CM交AB于点D,AB=9,AC=6,求AD的长.
分析 (1)根据尺规作图的方法,以AC为一边,在∠ACB的内部作∠ACM=∠ABC即可;
(2)根据△ACD与△ABC相似,运用相似三角形的对应边成比例进行计算即可.
解答 解:(1)如图所示,射线CM即为所求;
(2)∵∠ACD=∠ABC,∠CAD=∠BAC,
∴△ACD∽△ABC,
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$,即$\frac{AD}{6}$=$\frac{6}{9}$,
∴AD=4.
点评 本题主要考查了基本作图以及相似三角形的判定与性质的运用,解题时注意:两角对应相等的两个三角形相似;相似三角形的对应边成比例.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
8. 如图所示的几何体的俯视图为( )
如图所示的几何体的俯视图为( )
 如图所示的几何体的俯视图为( )
如图所示的几何体的俯视图为( )| A. |  | B. |  | C. |  | D. |  |
15.2的算术平方根是( )
| A. | $±\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | 2 |
12.-22=( )
| A. | -2 | B. | -4 | C. | 2 | D. | 4 |
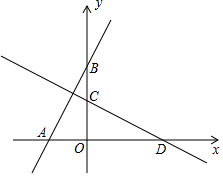 如图,在平面直角坐标系xOy中,过点A(-2,0)的直线交y轴正半轴于点B,将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D、C.
如图,在平面直角坐标系xOy中,过点A(-2,0)的直线交y轴正半轴于点B,将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D、C.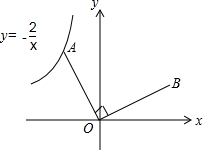 如图,已知点A是反比例函数y=-$\frac{2}{x}$的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为y=$\frac{2}{x}$.
如图,已知点A是反比例函数y=-$\frac{2}{x}$的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为y=$\frac{2}{x}$.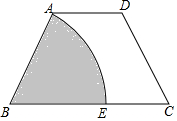 如图,四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是6π.
如图,四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是6π.