题目内容
8.若抛物线y=-x2+px+q与x轴交于A(a,0),B(b,0)两点,且a<1<b,则有( )| A. | p+q<1 | B. | p+q=1 | C. | p+q>1 | D. | pq>0 |
分析 由-1<0即可得出抛物线开口向下,再根据抛物线与x轴的两交点横坐标分别在1的两侧即可得出当x=1时,y=-1+p+q>0,移项后即可得出p+q>1.
解答 解:∵抛物线y=-x2+px+q中二次项系数为-1<0,
∴抛物线开口向下.
∵抛物线y=-x2+px+q与x轴交于A(a,0),B(b,0)两点,且a<1<b,
∴当x=1时,y=-1+p+q>0,
∴p+q>1.
故选C.
点评 本题考查了抛物线与x轴的交点以及二次函数图象与系数的关系,根据a<1<b找出“当x=1时,y=-1+p+q>0”是解题的关键.

练习册系列答案
相关题目
20.计算|-6|-(-$\frac{1}{3}$)0的值是( )
| A. | 5 | B. | -5 | C. | 5$\frac{2}{3}$ | D. | 7 |
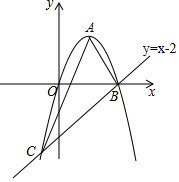 如图,已知抛物线y=-x2+2x经过原点O,且与直线y=x-2交于B,C两点.
如图,已知抛物线y=-x2+2x经过原点O,且与直线y=x-2交于B,C两点.