题目内容
18.在平面直角坐标系中,将抛物线y=2x2向上平移3个单位,得到的抛物线的函数表达式为y=2x2+3.分析 先确定抛物线y=2x2的顶点坐标为(0,0),再利用点平移的规律得到点(0,0)向上平移3个单位所得对应点的坐标,然后利用顶点式写出平移后抛物线的函数表达式.
解答 解:抛物线y=2x2的顶点坐标为(0,0),点(0,0)向上平移3个单位所得对应点的坐标为(0,3),
所以平移后抛物线的函数表达式为y=2x2+3.
故答案为y=2x2+3.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
9.下列说法正确的有( )
(1)带根号的数都是无理数;
(2)立方根等于本身的数是0和1;
(3)-a一定没有平方根;
(4)实数与数轴上的点是一一对应的;
(5)两个无理数的差还是无理数.
(1)带根号的数都是无理数;
(2)立方根等于本身的数是0和1;
(3)-a一定没有平方根;
(4)实数与数轴上的点是一一对应的;
(5)两个无理数的差还是无理数.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.下列各数精确到0.01的是( )
| A. | 5.1346≈5.135 | B. | 8.029≈8.0 | C. | 4.1974≈4.20 | D. | 0.6925≈0.693 |
3. 用一个平面按如图所示方法去截一个正方体,则截面是( )
用一个平面按如图所示方法去截一个正方体,则截面是( )
 用一个平面按如图所示方法去截一个正方体,则截面是( )
用一个平面按如图所示方法去截一个正方体,则截面是( )| A. |  | B. |  | C. |  | D. |  |
8.若抛物线y=-x2+px+q与x轴交于A(a,0),B(b,0)两点,且a<1<b,则有( )
| A. | p+q<1 | B. | p+q=1 | C. | p+q>1 | D. | pq>0 |
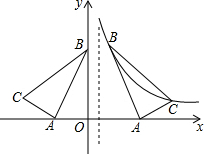 如图,在平面直角坐标系中有Rt△ABC,∠CAB=90°,A(-2,0),B(0,4),点C在第二象限且tan∠ACB=2,将Rt△ABC沿平行于y轴的某条直线翻折,得Rt△A1B1C1,若点B1,C1恰好落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则k的值等于$\frac{16}{3}$.
如图,在平面直角坐标系中有Rt△ABC,∠CAB=90°,A(-2,0),B(0,4),点C在第二象限且tan∠ACB=2,将Rt△ABC沿平行于y轴的某条直线翻折,得Rt△A1B1C1,若点B1,C1恰好落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则k的值等于$\frac{16}{3}$.