题目内容
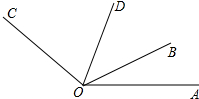 如图,∠BOC=4∠AOB,OD是∠AOC的平分线,∠BOD=42°,求∠AOB的度数.
如图,∠BOC=4∠AOB,OD是∠AOC的平分线,∠BOD=42°,求∠AOB的度数.考点:角平分线的定义
专题:
分析:设∠AOB=x,则∠BOC=4∠AOB=4x,∠AOC=∠AOB+∠BOC=5x.由OD是∠AOC的平分线,根据角平分线定义得出∠AOD=∠DOC=
∠AOC=
x,于是∠BOD=∠AOD-∠AOB=
x.根据∠BOD=42°,列出方程
x=42°,解方程即可.
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解答:解:设∠AOB=x,则∠BOC=4∠AOB=4x,∠AOC=∠AOB+∠BOC=5x.
∵OD是∠AOC的平分线,
∴∠AOD=∠DOC=
∠AOC=
x,
∴∠BOD=∠AOD-∠AOB=
x.
∵∠BOD=42°,
∴
x=42°,
∴x=28°,
即∠AOB=28°.
∵OD是∠AOC的平分线,
∴∠AOD=∠DOC=
| 1 |
| 2 |
| 5 |
| 2 |
∴∠BOD=∠AOD-∠AOB=
| 3 |
| 2 |
∵∠BOD=42°,
∴
| 3 |
| 2 |
∴x=28°,
即∠AOB=28°.
点评:本题考查了角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.设出适当的未知数x,列出关于x的方程是解题的关键.

练习册系列答案
相关题目
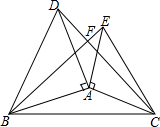 将等腰直角三角尺ABD、ACE如图放置,连接BE、CD.
将等腰直角三角尺ABD、ACE如图放置,连接BE、CD.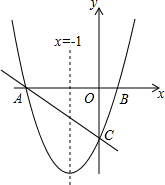 如图,抛物线y=ax2+bx+c的对称轴为x=-1,抛物线与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0).
如图,抛物线y=ax2+bx+c的对称轴为x=-1,抛物线与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0).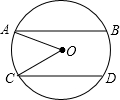 如图,在⊙O中,弦AB∥弦CD,且AB,CD位于圆心O的两侧,AB=8,CD=6,AB,CD之间的距离为7,连接OA,OC.
如图,在⊙O中,弦AB∥弦CD,且AB,CD位于圆心O的两侧,AB=8,CD=6,AB,CD之间的距离为7,连接OA,OC. 如图,数轴上点A表示
如图,数轴上点A表示 如图所示,菱形ABCD的对角线AC=8cm,BD=6cm,AC与BD相交于点O,求tan
如图所示,菱形ABCD的对角线AC=8cm,BD=6cm,AC与BD相交于点O,求tan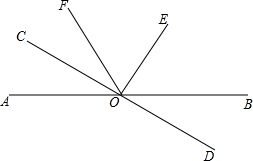 如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE.
如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE.