Question

9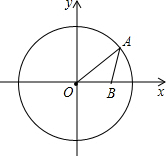．如图，在平面直角坐标系中，O为坐标原点，⊙O的半径为5，点B的坐标为（3，0），点A为⊙O上一动点，当∠OAB取最大值时，点A的坐标为（3，4）或（3，-4）．

Answer 1

分析 作OH⊥AB于H，如图，在Rt△OAH中，利用正弦的定义可判断当OH最大时，∠OAH最大，当OH=OB时，∠OAH最大，即A′B⊥OB时，∠OA′B最大，再根据勾股定理计算出A′B=4，
则A′（3，4），点A′关于x轴的对称点也满足条件，于是得到当∠OAB取最大值时，点A的坐标为（3，4）或（3，-4）．

解答 解：作OH⊥AB于H，如图，
在Rt△OAH中，∵sin∠OAH=$\frac{OH}{OA}$=$\frac{OH}{5}$，
∴当OH最大时，∠OAH最大，当OH=OB时，∠OAH最大，
即A′B⊥OB时，∠OA′B最大，
∴A′B=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴A′（3，4），
点A′关于x轴的对称点的坐标为（3，-4），
∴当∠OAB取最大值时，点A的坐标为（3，4）或（3，-4）．
故答案为（3，4）或（3，-4）．

点评 本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．