题目内容
7.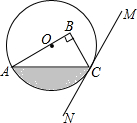 如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
分析 (1)MN是⊙O切线,只要证明∠OCM=90°即可.
(2)求出∠AOC以及BC,根据S阴=S扇形OAC-S△OAC计算即可.
解答 解:(1)MN是⊙O切线.
理由: 连接OC.
连接OC.
∵OA=OC,
∴∠OAC=∠OCA,
∵∠BOC=∠A+∠OCA=2∠A,∠BCM=2∠A,
∴∠BCM=∠BOC,
∵∠B=90°,
∴∠BOC+∠BCO=90°,
∴∠BCM+∠BCO=90°,
∴OC⊥MN,
∴MN是⊙O切线.
(2)由(1)可知∠BOC=∠BCM=60°,
∴∠AOC=120°,
在RT△BCO中,OC=OA=4,∠BCO=30°,
∴BO=$\frac{1}{2}$OC=2,BC=2$\sqrt{3}$
∴S阴=S扇形OAC-S△OAC=$\frac{120π•{4}^{2}}{360}$-$\frac{1}{2}$$•4•2\sqrt{3}$=$\frac{16π}{3}$-4$\sqrt{3}$.
点评 本题考查直线与圆的位置关系、扇形面积、三角形面积等知识,解题的关键是记住切线的判定方法,扇形的面积公式,属于中考常考题型.

练习册系列答案
相关题目
17.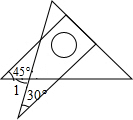 将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为( )
将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为( )
 将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为( )
将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为( )| A. | 75° | B. | 65° | C. | 45° | D. | 30° |
18.2016元旦小长假三天,江西共计接待省内外游客约1040万人,其中1040万用科学记数法可表示为( )
| A. | 0.104×108 | B. | 1.04×107 | C. | 10.4×106 | D. | 104×105 |
2.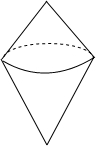 如图所示的几何体左视图是( )
如图所示的几何体左视图是( )
 如图所示的几何体左视图是( )
如图所示的几何体左视图是( )| A. | 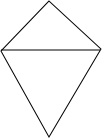 | B. | 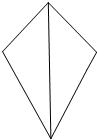 | C. | 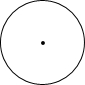 | D. |  |
19.下列式子错误的是( )
| A. | cos40°=sin50° | B. | tan15°•tan75°=1 | ||
| C. | sin225°+cos225°=1 | D. | sin60°=2sin30° |
16.下列各式变形中,正确的是( )
| A. | x2•x3=x6 | B. | $\sqrt{{x}^{2}}$=|x| | C. | (x2-$\frac{1}{x}$)÷x=x-1 | D. | x2-x+1=(x-$\frac{1}{2}$)2+$\frac{1}{4}$ |
11.下列多项式中,可以用平方差公式分解因式的是( )
| A. | x2+1 | B. | -x2-1 | ||
| C. | $\frac{1}{9}{x}^{2}-1$ | D. | 以上答案都不正确 |