题目内容
17.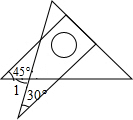 将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为( )
将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为( )| A. | 75° | B. | 65° | C. | 45° | D. | 30° |
分析 先根据同旁内角互补,两直线平行得出AC∥DF,再根据两直线平行内错角相等得出∠2=∠A=45°,然后根据三角形内角与外角的关系可得∠1的度数.
解答  解:∵∠ACB=∠DFE=90°,
解:∵∠ACB=∠DFE=90°,
∴∠ACB+∠DFE=180°,
∴AC∥DF,
∴∠2=∠A=45°,
∴∠1=∠2+∠D=45°+30°=75°.
故选A.
点评 本题考查了平行线的判定与性质,三角形外角的性质,求出∠2=∠A=45°是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知三角形斜边的长是8,则斜边上的中线长为( )
| A. | 16 | B. | 12 | C. | 4 | D. | 2 |
8.有一种病毒呈球形,其最小直径约为0.000 000 08米,用科学记数法表示为( )
| A. | 80×10-9米 | B. | 0.8×10-7米 | C. | 8×10-8米 | D. | 8×10-9米 |
5.进入春季后,杨树、柳树飞絮影响着人们的生活,本市将对现有的2000000棵杨、柳树雌株进行治理,减少飞絮现象.将2000000用科学记数法表示为( )
| A. | 2×107 | B. | 2×106 | C. | 20×105 | D. | 200×104 |
2.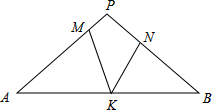 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )| A. | 44° | B. | 66° | C. | 88° | D. | 92° |
6. 如图,?ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
如图,?ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
 如图,?ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
如图,?ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )| A. | 10 | B. | 14 | C. | 20 | D. | 22 |
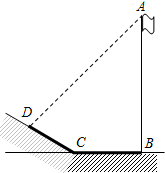 为了测量操场边上旗杆的高度,学习小组在一个阳光明媚的时候带着测量工具来到旗杆下,此时发现旗杆顶端A的影子落在旗杆附近一段坡角为30°的斜坡上的点D处,并测得太阳光线与斜坡的夹角∠ADC=75°,旗杆影子落在操场上的长BC=5米,落在斜坡上的长CD=6米.
为了测量操场边上旗杆的高度,学习小组在一个阳光明媚的时候带着测量工具来到旗杆下,此时发现旗杆顶端A的影子落在旗杆附近一段坡角为30°的斜坡上的点D处,并测得太阳光线与斜坡的夹角∠ADC=75°,旗杆影子落在操场上的长BC=5米,落在斜坡上的长CD=6米.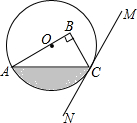 如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.