题目内容
6.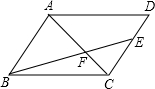 如图,在?ABCD中,点E在DC上,EC=2DE,若AC与BE相交于点F,AC=10,则FC=4.
如图,在?ABCD中,点E在DC上,EC=2DE,若AC与BE相交于点F,AC=10,则FC=4.
分析 根据平行四边形的性质得到AB=CD,由已知条件得到CE:CD=CE:AB=2:3,通过△ABF∽△CEF,得到$\frac{CE}{AB}=\frac{CF}{AF}$=$\frac{2}{3}$,于是得到结论.
解答 解:在?ABCD中,
∵AB=CD,
∵EC=2DE,
∴CE:CD=CE:AB=2:3,
∵AB∥CD,
∴△ABF∽△CEF,
∴$\frac{CE}{AB}=\frac{CF}{AF}$=$\frac{2}{3}$,
∴$\frac{CF}{AC}$=$\frac{2}{5}$,
∵AC=10,
∴CF=4.
故答案为:4.
点评 本题考查了平行四边形的性质、相似三角形的判定和性质,熟练掌握相似三角形的判定定理是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
16.若点A(x1,y1),B(x2,y2),和C(x3,y3),分别在反比例函数$y=\frac{6}{x}$的图象上,且x1<x2<0<x3,则下列判断中正确的是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y2<y1 | D. | y2<y3<y1 |
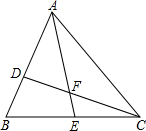 如图,点D在△ABC边AB上且AD:BD=2:1,E是BC的中点,设S1为△ADF的面积,S2为△CEF的面积.若S△ABC=24,则S1-S2=4.
如图,点D在△ABC边AB上且AD:BD=2:1,E是BC的中点,设S1为△ADF的面积,S2为△CEF的面积.若S△ABC=24,则S1-S2=4.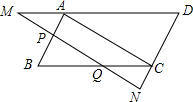 已知:?ABCD中,直线MN∥AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q.求证:PM=QN.
已知:?ABCD中,直线MN∥AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q.求证:PM=QN.