题目内容
11.(1)计算:[(4b+3a)(3a-4b)-(b-3a)2]÷4b(2)先化简,再求值.(2x-1)(2x+1)-(x-2)2-(x+2)2,其中,x=-3$\frac{1}{3}$.
分析 (1)先利用完全平方公式和平方差公式计算合并,再进一步计算除法即可;
(2)先利用完全平方公式和平方差公式计算合并,再进一步代入求得答案即可.
解答 解:(1)原式=(9a2-16b2-b2+6ab-9a2)÷4b
=(-17b2+6ab)÷4b
=-$\frac{17}{4}$b+$\frac{3}{2}$a;
(2)原式=4x2-1-x2+4x-4-x2-4x-4
=2x2-9,
当x=-3$\frac{1}{3}$时,
原式=2×$\frac{100}{9}$-9=$\frac{119}{9}$.
点评 此题考查整式的化简求值,正确利用计算公式和计算方法计算合并是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1. 如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=42°,则∠BAD=( )°.
如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=42°,则∠BAD=( )°.
 如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=42°,则∠BAD=( )°.
如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=42°,则∠BAD=( )°.| A. | 42 | B. | 48 | C. | 60 | D. | 45 |
2.已知当x=2时,反比例函数y=$\frac{{k}_{1}}{x}$与正比例函数y=k2x的值相等,则k1:k2的值是( )
| A. | $\frac{1}{4}$ | B. | 1 | C. | 2 | D. | 4 |
19.已知ab>0,bc<0,化简:$\sqrt{-\frac{{a}^{3}{c}^{3}}{{b}^{3}}}$的结果为( )
| A. | $\frac{ac}{{b}^{2}}$$\sqrt{abc}$ | B. | $\frac{ac}{{b}^{2}}$$\sqrt{-abc}$ | C. | -$\frac{ac}{{b}^{2}}$$\sqrt{-abc}$ | D. | -$\frac{ac}{{b}^{2}}$$\sqrt{abc}$ |
3.一次函数y=kx+b与反比例函数y=$\frac{m}{x}$中,若x与y的部分对应值如表:
则关于x的不等式$\frac{m}{x}$≤kx+b的解集是x≤-1或0<x≤3.
| x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
| y=kx+b | … | 5 | 4 | 3 | 1 | 0 | -1 | … |
| y=$\frac{m}{x}$ | … | 1 | $\frac{3}{2}$ | 3 | -3 | -$\frac{3}{2}$ | -1 | … |
1.下列运算正确的是( )
| A. | a•a2=a2 | B. | (ab)2=ab2 | C. | (a2)3=a6 | D. | a10÷a2=a5 |
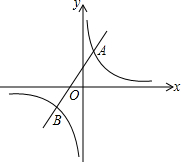 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于点A(1,4),点B(m,-2)
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于点A(1,4),点B(m,-2)