题目内容
1．
如图，AB为⊙O的直径，CD为⊙O的弦，∠ACD=42°，则∠BAD=（ ）°．| A． | 42 | B． | 48 | C． | 60 | D． | 45 |
分析 连接BD，根据∠ACD=42°，可得∠ABD=90°-42°，然后根据AB为直径，得出∠ADB=90°，继而可求得∠BAD．
解答 解：连接BD，
∵∠ACD=42°，
∴∠ABD=42°，
∵AB为直径，
∴∠ADB=90°，
∴∠BAD=890°-∠ABD=48°．
故选B．
点评 本题考查了圆周角定理，解答本题的关键是掌握圆周角定理中在同圆或等圆中，同弧或等弧所对的圆周角相等．
练习册系列答案
名校课堂系列答案
相关题目
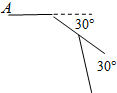如图，王老师在上多边形外角和这节课时，做了一个活动，让小明在操场上从A点出发前进1m，向右转30°，再前进1m，又向右转30°，…，这样一直走下去，直到他第一次回到出发点A为止，他所走的路径构成了一个多边形．小明一共走了12m，这个多边形的内角和是1800度．