题目内容
已知m是方程x2-x-2=0的一个实数根,求代数式(m2-m)•(m-
+2014)的值.
| 2 |
| m |
考点:一元二次方程的解
专题:
分析:把x=m代入已知方程,得到m2-m=2,m2-2=m,然后代入所求的代数式进行求值即可.
解答:解:∵m是方程x2-x-2=0的一个实数根,
∴m2-m-2=0,
∴m2-m=2,m2-2=m,
∴(m2-m)•(m-
+2014)=2×(
+2014)=2×(
+2014)=4030.
∴m2-m-2=0,
∴m2-m=2,m2-2=m,
∴(m2-m)•(m-
| 2 |
| m |
| m2-2 |
| m |
| m |
| m |
点评:本题考查了一元二次方程的解的定义.注意“整体代入”思想的应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
下列各式中最简分式是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
某药品经过两次降价,每瓶零售价由100元降为81元,若每次平均降价的百分率为x,则下列方程正确的是( )
| A、100x2=81 |
| B、100(1-x)2=81 |
| C、100(1+x)2=81 |
| D、81(1-x)2=100 |
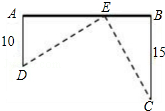 如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.则E应建在距A
如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.则E应建在距A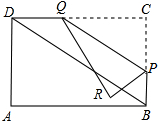 如图,在矩形ABCD中,AB=9,AD=3
如图,在矩形ABCD中,AB=9,AD=3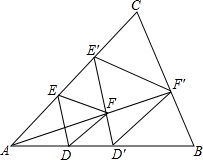 等边三角形的三个顶点分别在一个三角形的三条边上,我们称这个三角形为这个三角形的“内接等边三角形”,
等边三角形的三个顶点分别在一个三角形的三条边上,我们称这个三角形为这个三角形的“内接等边三角形”,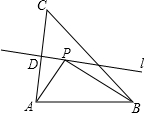 如图,AC的垂直平分线l交AC于点D,BC=4,点P在直线l上,则PB+PA的最小值是
如图,AC的垂直平分线l交AC于点D,BC=4,点P在直线l上,则PB+PA的最小值是