题目内容
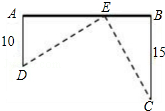如图，在笔直的铁路上A、B两点相距25km，C、D为两村庄，DA=10km，CB=15km，DA⊥AB于A，CB⊥AB于B，现要在AB上建一个中转站E，使得C、D两村到E站的距离相等．则E应建在距A考点：勾股定理的应用
专题：
分析：利用DE=CE，再结合勾股定理求出即可．
解答：解：设AE=xkm，则BE=（25-x）km，根据题意可得：
∵DE=CE，
∴AD2+AE2=BE2+BC2，
故102+x2=（25-x）2+152，
解得；x=15．
故答案为：15．
∵DE=CE，
∴AD2+AE2=BE2+BC2，
故102+x2=（25-x）2+152，
解得；x=15．
故答案为：15．
点评：此题主要考查了勾股定理的应用，利用DE=CE得出是解题关键．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
已知一次函数y=kx+b的图象经过二、三、四象限，则（ ）
| A、k＞0，b＞0 |
| B、k＞0，b＜0 |
| C、k＜0，b＞0 |
| D、k＜0，b＜0 |
已知正比例函数y=kx（k＜0）的图象上两点A（x1，y1）、B（x2，y2），且x1＜x2，下列说法正确的是（ ）
| A、y1＞y2 |
| B、y1＜y2 |
| C、y1=y2 |
| D、不能确定 |
一元二次方程x2+x-6=0的解是（ ）
| A、x1=-2，x2=3 |
| B、x1=2，x2=-3 |
| C、x1=-1，x2=6 |
| D、x1=1，x2=-6 |
用四舍五入法按要求对5.01923分别取近似值，其中正确的是（ ）
| A、5.0×105（精确到十分位） |
| B、5.01（精确到百分位） |
| C、5.02（精确到千分位） |
| D、5.019（精确到0.001） |
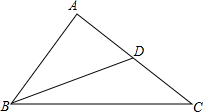如图，AB=4，BC=6，BD为△ABC的中线，求BD的范围．