题目内容
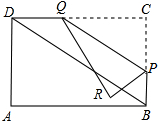 如图,在矩形ABCD中,AB=9,AD=3
如图,在矩形ABCD中,AB=9,AD=3| 3 |
考点:翻折变换(折叠问题),矩形的性质
专题:
分析:如图,首先作辅助线构造相似三角形;然后借助平行线分线段成比例定理、相似三角形的判定及其性质求出线段BR的长度;借助勾股定理即可求出CP的长.
解答: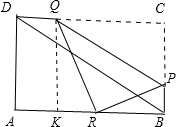 解:如图,当点R落在矩形ABCD的AB边上时,
解:如图,当点R落在矩形ABCD的AB边上时,
过点Q作QK⊥AB于点K;
∵四边形ABCD为矩形,
∴四边形QKBC也为矩形,
∴QK=BC=AD=3
;
由题意知:△QRP≌△QCP,
∴RP=CP(设为x),QR=QC(设为y),
∠QRP=∠C=90°;
∵PQ∥BD,
∴
=
,而DC=AB=9,BC=AD=3
,
∴
=
=
;
∵∠QKR=∠QRP=∠RBP=90°,
∴∠KQR+∠QRK=∠QRK+∠PRB,
∴∠KQR=∠PRB,
∴△QKR∽△RBP,
∴
=
,而
=
=
,QK=3
,
∴RP=3;在直角△BRP中,
由勾股定理得:RP2=RB2+BP2,
即x2=32+(3
-x)2,
解得:x=2
,
故该题答案为2
.
 解:如图,当点R落在矩形ABCD的AB边上时,
解:如图,当点R落在矩形ABCD的AB边上时,过点Q作QK⊥AB于点K;
∵四边形ABCD为矩形,
∴四边形QKBC也为矩形,
∴QK=BC=AD=3
| 3 |
由题意知:△QRP≌△QCP,
∴RP=CP(设为x),QR=QC(设为y),
∠QRP=∠C=90°;
∵PQ∥BD,
∴
| QC |
| DC |
| PC |
| BC |
| 3 |
∴
| y |
| x |
| 9 | ||
3
|
| 3 |
∵∠QKR=∠QRP=∠RBP=90°,
∴∠KQR+∠QRK=∠QRK+∠PRB,
∴∠KQR=∠PRB,
∴△QKR∽△RBP,
∴
| QR |
| RP |
| QK |
| RB |
| QR |
| RP |
| y |
| x |
| 3 |
| 3 |
∴RP=3;在直角△BRP中,
由勾股定理得:RP2=RB2+BP2,
即x2=32+(3
| 3 |
解得:x=2
| 3 |
故该题答案为2
| 3 |
点评:该命题以矩形为载体,以旋转变换为方法,在考查旋转变换的性质及其应用问题的同时,还渗透了对矩形的性质、相似三角形的判定及其性质等几何知识点的考查;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
用四舍五入法按要求对5.01923分别取近似值,其中正确的是( )
| A、5.0×105(精确到十分位) |
| B、5.01(精确到百分位) |
| C、5.02(精确到千分位) |
| D、5.019(精确到0.001) |
36.33°可化成( )
| A、36°30′3″ |
| B、36°3′ |
| C、36°30′30″ |
| D、36°19′48″ |
 按要求画图,并描述所作线段.
按要求画图,并描述所作线段.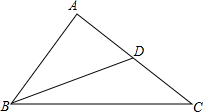 如图,AB=4,BC=6,BD为△ABC的中线,求BD的范围.
如图,AB=4,BC=6,BD为△ABC的中线,求BD的范围.