题目内容
4. 如图,△APB中,AB=2,∠APB=90°,在AB的同侧作正△ABD、正△APE和正△BPC,则四边形PCDE面积的最大值是1.
如图,△APB中,AB=2,∠APB=90°,在AB的同侧作正△ABD、正△APE和正△BPC,则四边形PCDE面积的最大值是1.
分析 先延长EP交BC于点F,得出PF⊥BC,再判定四边形CDEP为平行四边形,根据平行四边形的性质得出:四边形CDEP的面积=EP×CF=a×$\frac{1}{2}$b=$\frac{1}{2}$ab,最后根据a2+b2=4,判断$\frac{1}{2}$ab的最大值即可.
解答  解:延长EP交BC于点F,
解:延长EP交BC于点F,
∵∠APB=90°,∠APE=∠BPC=60°,
∴∠EPC=150°,
∴∠CPF=180°-150°=30°,
∴PF平分∠BPC,
又∵PB=PC,
∴PF⊥BC,
设Rt△ABP中,AP=a,BP=b,则
CF=$\frac{1}{2}$CP=$\frac{1}{2}$b,a2+b2=22=4,
∵△APE和△ABD都是等边三角形,
∴AE=AP,AD=AB,∠EAP=∠DAB=60°,
∴∠EAD=∠PAB,
∴△EAD≌△PAB(SAS),
∴ED=PB=CP,
同理可得:△APB≌△DCB(SAS),
∴EP=AP=CD,
∴四边形CDEP是平行四边形,
∴四边形CDEP的面积=EP×CF=a×$\frac{1}{2}$b=$\frac{1}{2}$ab,
又∵(a-b)2=a2-2ab+b2≥0,
∴2ab≤a2+b2=4,
∴$\frac{1}{2}$ab≤1,
即四边形PCDE面积的最大值为1.
故答案为:1
点评 本题主要考查了等边三角形的性质、平行四边形的判定与性质以及全等三角形的判定与性质,解决问题的关键是作辅助线构造平行四边形的高线.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
16.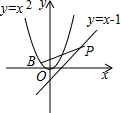 如图,点P在直线y=x-1上,若存在过点P的直线交抛物线y=x2于A、B两点,且PA=AB,则称点P为“优点”,下列结论中正确的是( )
如图,点P在直线y=x-1上,若存在过点P的直线交抛物线y=x2于A、B两点,且PA=AB,则称点P为“优点”,下列结论中正确的是( )
 如图,点P在直线y=x-1上,若存在过点P的直线交抛物线y=x2于A、B两点,且PA=AB,则称点P为“优点”,下列结论中正确的是( )
如图,点P在直线y=x-1上,若存在过点P的直线交抛物线y=x2于A、B两点,且PA=AB,则称点P为“优点”,下列结论中正确的是( )| A. | 直线y=x-1上的所有点都是“优点” | |
| B. | 直线y=x-1上仅有有限个点是“优点” | |
| C. | 直线y=x-1上的所有点都不是“优点” | |
| D. | 直线y=x-1上有无穷多个点(不是所有的点)是“优点” |
 如图,ABCD是正方形,过点A的直线依次与BD、DC及BC的延长线交于E、F、G,若AE=3cm,EF=2cm,则FG=2.5cm.
如图,ABCD是正方形,过点A的直线依次与BD、DC及BC的延长线交于E、F、G,若AE=3cm,EF=2cm,则FG=2.5cm. 已知如图所示△ABC中,∠ACB=90°,AC=BC,点P在△ABC内,且PA=$\sqrt{3}$,PB=1,PC=1,则∠BPC=135°.
已知如图所示△ABC中,∠ACB=90°,AC=BC,点P在△ABC内,且PA=$\sqrt{3}$,PB=1,PC=1,则∠BPC=135°.