题目内容
14.(1)解方程:2x2+5x=3(2)解不等式组$\left\{\begin{array}{l}{3x+4>x}\\{\frac{4}{3}x≤x+\frac{2}{3}}\end{array}\right.$.
分析 (1)先把方程化为一般式,然后利用因式分解法解方程;
(2)分别解两个不等式得到x>-2和x≤2,然后根据大小小大中间找确定不等式组的解集.
解答 解:(1)原方程可化为2x2+5x-3=0,
(2x-1)(x+3)=0,
2x-1=0或x+3=0,
所以x1=$\frac{1}{2}$,x2=-3;
(2)$\left\{\begin{array}{l}{3x+4>x①}\\{\frac{4}{3}x≤x+\frac{2}{3}②}\end{array}\right.$,
由①得x>-2,
由②得:x≤2,
∴不等式组的解集为:-2<x≤2.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.也考查了解一元一次不等式组.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.关于x的一元二次方程x2-ax-1=0(其中a为常数)的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 可能有实数根,也可能没有实数根 | ||
| C. | 有两个相等的实数根 | D. | 没有实数根 |
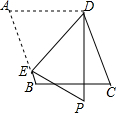 如图,在平行四边形ABCD中,点E为AB边上一点,将△AED沿直线DE翻折,点A落在点P处,且DP⊥BC,则∠EDP=45°.
如图,在平行四边形ABCD中,点E为AB边上一点,将△AED沿直线DE翻折,点A落在点P处,且DP⊥BC,则∠EDP=45°.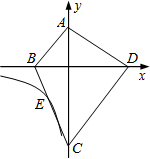 如图,四边形ABCD的顶点都在坐标轴上,若AB∥CD,△ABD与△ACD的面积分别为20和30,若双曲线y=$\frac{k}{x}$恰好经过BC的中点E,则k的值为( )
如图,四边形ABCD的顶点都在坐标轴上,若AB∥CD,△ABD与△ACD的面积分别为20和30,若双曲线y=$\frac{k}{x}$恰好经过BC的中点E,则k的值为( )