题目内容
2．
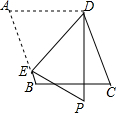如图，在平行四边形ABCD中，点E为AB边上一点，将△AED沿直线DE翻折，点A落在点P处，且DP⊥BC，则∠EDP=45°．
分析 根据平行线的性质得到∠ADC+∠C=180°，根据垂直的定义得到∠C+∠CDP=90°，根据折叠的性质得到∠ADE=∠PDE，于是得到结论．
解答 解：∵在平行四边形ABCD中，AD∥BC，
∴∠ADC+∠C=180°，
∵DP⊥BC，
∴∠C+∠CDP=90°，
∴∠ADE+∠PDE=90°，
∵将△AED沿直线DE翻折，点A落在点P处，
∴∠ADE=∠PDE，
∴∠PDE=45°，
故答案为：45．
点评 本题考查了平行四边形的性质，翻折变换（折叠问题），熟练掌握折叠的性质是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
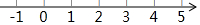解不等式组$\left\{\begin{array}{l}{\frac{1}{2}x＞1，①}\\{1-x≥-3，②}\end{array}\right.$
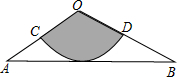如图，从一张腰长为6cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，用剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥底面半径为1cm．