题目内容
1．
如图所示：已知O为AB上一点，∠BOC=46°，OD平分∠AOC，∠AOD=67°．
分析 根据平角的定义求出∠AOC的度数，再根据角平分线的性质即可得出答案．
解答 解：∵∠BOC=46°，
∴∠AOC=134°，
∵OD平分∠AOC，
∴∠AOD=∠COD，
∴∠AOD=67°；
故答案为：67°．
点评 此题考查了角平分线的性质，根据平角的定义求出∠AOC的度数是本题的关键，是一道基础题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
12．
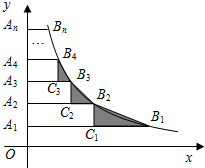如图，在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An（n为正整数），过A1，A2，A3，…，An分别作x轴的平行线，与反比例函数y=$\frac{2}{x}$（x＞0）交于点B1，B2，B3，…，Bn，如图所示的Rt△B1C1B2，Rt△B2C2B3，Rt△B3C3B4，…，Rt△Bn-1Cn-1Bn面积分别记为S1，S2，S3，…，Sn-1，则S1+S2+S3+…+Sn-1=（ ）
如图，在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An（n为正整数），过A1，A2，A3，…，An分别作x轴的平行线，与反比例函数y=$\frac{2}{x}$（x＞0）交于点B1，B2，B3，…，Bn，如图所示的Rt△B1C1B2，Rt△B2C2B3，Rt△B3C3B4，…，Rt△Bn-1Cn-1Bn面积分别记为S1，S2，S3，…，Sn-1，则S1+S2+S3+…+Sn-1=（ ）| A． | 1 | B． | 2 | C． | 1-$\frac{1}{n}$ | D． | 2-$\frac{1}{n}$ |
6．下列二次根式中，最简二次根式是（ ）
| A． | $\sqrt{12}$ | B． | $\sqrt{x-3}$ | C． | $\sqrt{\frac{3}{2}}$ | D． | $\sqrt{{a^2}b}$ |
10．如图由圆形组成的四个图形中，可以看做是中心对称图形的有（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |