题目内容
6.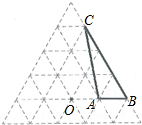 如图是由边长为1的小正三角形组成的网格图,点O和△ABC的顶点都在正三角形的格点上,将△ABC绕点O逆时针旋转120°得到△A′B′C′.
如图是由边长为1的小正三角形组成的网格图,点O和△ABC的顶点都在正三角形的格点上,将△ABC绕点O逆时针旋转120°得到△A′B′C′.(1)在网格中画出旋转后的△A′B′C′;
(2)求AB边旋转时扫过的面积.
分析 (1)利用网格特点、等边三角形的性质和旋转的性质画出点A、B、C的对应点A′、B′、C,从而得到△A′B′C′;
(2)根据扇形的面积公式,利用AB边旋转时扫过的面积=S扇形BOB′-S扇形AOA′进行计算即可.
解答 解:(1)如图,△A′B′C′为所作;
(2)AB边旋转时扫过的面积=S扇形BOB′-S扇形AOA′
=$\frac{120•π•{2}^{2}}{360}$-$\frac{120•π•{1}^{2}}{360}$
=π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
14.来自宁波轨道交通部门的统计数据显示,轨道2号线开通30天,轨道1号线和2号线的总客流量约663万人次,将数据663万用科学记数法表示为( )
| A. | 0.663×107 | B. | 663×104 | C. | 6.63×107 | D. | 6.63×106 |
11.据邵东县2016年政府工作报告显示,邵东县2015年财政总收入为18.94亿元,18.94亿元用科学记数法表示为( )元.
| A. | 18.948 | B. | 18.94×108 | C. | 1.894×109 | D. | 1.894×1010 |
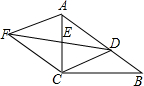 如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点(点D不与点A重合),点E是AC的中点,连结DE并延长至点F,使EF=DE,连结AF、CF.
如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点(点D不与点A重合),点E是AC的中点,连结DE并延长至点F,使EF=DE,连结AF、CF. 画图并填空:
画图并填空: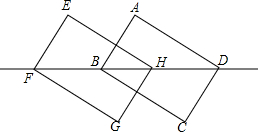 如图,在长方形ABCD中,AB=CD=6,AD=BC=8,对角线BD=10,现将长方形沿对角线BD所在直线向左平移4个单位得到长方形EFGH,则点F到直线AD的距离是( )
如图,在长方形ABCD中,AB=CD=6,AD=BC=8,对角线BD=10,现将长方形沿对角线BD所在直线向左平移4个单位得到长方形EFGH,则点F到直线AD的距离是( )