题目内容
13. 如图,在平面直角坐标系中,点A的坐标为(4,0),点P(x,y)是直线y=-x+6上一动点,O是坐标原点.
如图,在平面直角坐标系中,点A的坐标为(4,0),点P(x,y)是直线y=-x+6上一动点,O是坐标原点.(1)求△OPA的面积S与x的函表达式;
(2)当P点坐标为多少时,S=10?
(3)在直线y=-x+6上求一点Q,使△QOA是以OA为底边的等腰三角形;(在图中作出Q点,并写出Q点坐标)
(4)在直线y=-x+6上点M的坐标,使△MOA是以OA为直角边的直角三角形.
分析 (1)根据题意求出OA的长,根据一次函数的性质和三角形面积公式列出△OPA的面积S与x的函数关系式;
(2)把S=10代入关系式,解方程即可;
(3)根据线段垂直平分线的性质和作法进行解答;
(4)分∠MOA=90°和∠OAM两种情况,根据一次函数的性质解答即可.
解答 解:(1)∵点A(4,0),O是坐标原点,
∴OA=4,
∵点P(x,y)是第一象限直线y=-x+6上的点,
∴S=$\frac{1}{2}$×OA×y=$\frac{1}{2}$×4×(-x+6)=-2x+12;
(2)当S=10时,-2x+12=10,
∴x=1,y=-x+6=5,
∴P(1,5);
(3) 作线段OA的垂直平分线交直线y=-x+6于点Q,则点Q即为所求,
作线段OA的垂直平分线交直线y=-x+6于点Q,则点Q即为所求,
∵OA=4,
∴点Q的横坐标为2,
当x=2时,y=-x+6=4,
则点Q的坐标为(2,4);
(4)当∠MOA=90°时,点M的坐标为(0,4),
当∠OAM=90°时,点M的横坐标为4,
则y=-x+6=2,
点M的坐标为(4,2).
点评 本题考查的是一次函数图象和性质、坐标与图形的关系以及线段垂直平分线的性质,根据题意列出函数关系式是解题的关键,注意分情况讨论思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列各式中,正确的是( )
| A. | $\frac{-x+y}{-x-y}$=$\frac{x-y}{x+y}$ | B. | $\frac{-x+y}{x-y}$=$\frac{-x-y}{x-y}$ | C. | $\frac{-x+y}{-x-y}$=$\frac{x+y}{x-y}$ | D. | $\frac{-x+y}{x-y}$=$\frac{x-y}{x+y}$ |
3.单项式-$\frac{3{a}^{2}{b}^{4}}{5}$的系数和次数分别是( )
| A. | $\frac{3}{5}$和6 | B. | -$\frac{3}{5}$和6 | C. | -3和6 | D. | -$\frac{1}{5}$和6 |
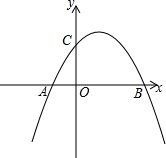 如图:已知二次函数y=-x2+bx+c图象分别交x轴于A(-$\frac{1}{2}$,0)、B($\sqrt{5}$,0)两点,交y轴于点C,过B、C两点作直线BC.
如图:已知二次函数y=-x2+bx+c图象分别交x轴于A(-$\frac{1}{2}$,0)、B($\sqrt{5}$,0)两点,交y轴于点C,过B、C两点作直线BC.