题目内容
7.点A(2m+1,m+2)在第二象限内,且点A的横坐标、纵坐标均为整数,则点A的坐标为(-1,1).分析 根据第二象限内点的横坐标小于零,纵坐标大于零,可得不等式组,根据解不等式组,可得答案.
解答 解:由A(2m+1,m+2)在第二象限内,得
$\left\{\begin{array}{l}{2m+1<0}\\{m+2>0}\end{array}\right.$,
解得-2<m<-$\frac{1}{2}$,
点A的横坐标、纵坐标均为整数,得
m=-1.
2m+1=-1,m+2=1,
则点A的坐标为(-1,1),
故答案为:(-1,1).
点评 本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列命题中,假命题是( )
| A. | 如果两条直线都与第三条直线平行,那么这两条直线也互相平行 | |
| B. | 两条直线被第三条直线所截,同旁内角互补 | |
| C. | 两直线平行,内错角相等 | |
| D. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 |
 甲、乙两辆汽车沿同一路线赶赴距出发地450千米的目的地,图中折线OABC和线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的关系,根据图象回答下列问题:
甲、乙两辆汽车沿同一路线赶赴距出发地450千米的目的地,图中折线OABC和线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的关系,根据图象回答下列问题: 已知:如图,AB=CD,AB∥CD,FD∥EB 求证:CE=AF.
已知:如图,AB=CD,AB∥CD,FD∥EB 求证:CE=AF.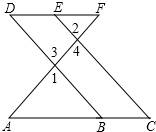 完成下面的证明.
完成下面的证明.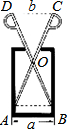 如图,质地均匀的空心圆柱形零件的外直径为a,现用一个交叉钳(AC和BD的长相等)测量,如果$\frac{OA}{OC}=\frac{OB}{OD}=n$,而且CD=b,那么这个零件的厚度为$\frac{a-bn}{2}$.
如图,质地均匀的空心圆柱形零件的外直径为a,现用一个交叉钳(AC和BD的长相等)测量,如果$\frac{OA}{OC}=\frac{OB}{OD}=n$,而且CD=b,那么这个零件的厚度为$\frac{a-bn}{2}$. 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数.