题目内容
10．计算：$\sqrt{54}$$÷\sqrt{3}$+$\sqrt{8}$=5$\sqrt{2}$．分析 先计算二次根式的除法，再化简二次根式，最后合并即可．
解答 解：原式=$\sqrt{18}$+$\sqrt{8}$
=3$\sqrt{2}$+2$\sqrt{2}$
=5$\sqrt{2}$，
故答案为：5$\sqrt{2}$．
点评 本题主要考查二次根式的混合运算，熟练掌握二次根式的运算法则是解题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
1．线段CD是由线段AB平移得到的，点A（-2，5）的对应点为C（3，7），则点B（-4，-7）的对应点D的坐标为（ ）
| A． | （2，9） | B． | （5，2） | C． | （1，-5） | D． | （-9，-5） |
如图，在?ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF，CF．在不添加辅助线的情况下，请写出与∠AEF相等的所有角∠DCF，∠BCF，∠DFC．
15．在实数3.1415926，$\sqrt{8}$，$\root{3}{27}$，1.010010001…，$\frac{22}{7}$，π，4.$\stackrel{•}{2}\stackrel{•}{1}$中，无理数有（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
如图，△ABC≌△DEF，点A、B、C对应点为D、E、F，若BE=3，AE=1，则DE=4．
20．
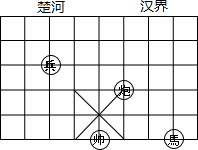如图，若在象棋盘上建立直角坐标系，使“帥”位于点（-1，-2），“馬”位于点（2，-2），则“炮”位于点（ ）
如图，若在象棋盘上建立直角坐标系，使“帥”位于点（-1，-2），“馬”位于点（2，-2），则“炮”位于点（ ）| A． | （0，1 ） | B． | （0，-1） | C． | （0，0） | D． | （1，0） |