题目内容
2.某网店试营销一种新产品,进价为20元/件,试营销期为18天,销售价y(元/件)与销售时间x(天)满足:当10≤x≤18时,y=k1x+30;当1≤x≤9时,y=$\frac{{k}_{2}}{x}$+20.在试营销期间,销售量p=30-x;已知当x=5或12时,y=32.5(1)求k1,k2的值;
(2)求该网店的销售利润w(元)与销售天数x(天)之间的函数关系式;
(3)网店试营销期间,第几天获得的利润最大?最大利润是多少?
分析 (1)根据题意可以分别求出k1,k2的值;
(2)由题意可以得到该网店的销售利润w(元)与销售天数x(天)之间的函数关系式;
(3)根据第二问求得的函数关系式分别讨论可以求得第几天获得最大利润,同时可以求得最大利润是多少.
解答 解;(1)∵当x=5或12时,y=32.5,
∴$32.5=\frac{{k}_{2}}{5}+20$或32.5=k1×12+30,
解得,${k}_{1}=\frac{5}{24},{k}_{2}=62.5$,
即,${k}_{1}=\frac{5}{24},{k}_{2}=62.5$;
(2)由题意可得,
w=$\left\{\begin{array}{l}{(\frac{62.5}{x}+20-20)×(30-x)(1≤x≤9)}\\{(\frac{5}{24}x+30-20)×(30-x)(10≤x≤18)}\end{array}\right.$
化简,得
w=$\left\{\begin{array}{l}{\frac{1875}{x}-62.5(1≤x≤9)}\\{-\frac{5}{24}{x}^{2}-\frac{15}{4}x+300(10≤x≤18)}\end{array}\right.$
即该网店的销售利润w(元)与销售天数x(天)之间的函数关系式是:w=$\left\{\begin{array}{l}{\frac{1875}{x}-62.5(1≤x≤9)}\\{-\frac{5}{24}{x}^{2}-\frac{15}{4}x+300(10≤x≤18)}\end{array}\right.$;
(3)当1≤x≤9时,$w=\frac{1875}{x}-62.5$中w随x的增大而减小,故x=1时,w取到最大,此时w=$\frac{1875}{1}-62.5=1812.5$(元),
当10≤x≤18时,$w=-\frac{5}{24}{x}^{2}-\frac{15}{4}x+300$的对称轴为:x=$-\frac{-\frac{15}{4}}{2×(-\frac{5}{24})}=-9$,
当x>-9时,w随x的增大而减小,故当x=10时取得最大值,此时w=$-\frac{5}{24}×1{0}^{2}-\frac{15}{4}×10+300$=$\frac{725}{3}$(元),
∵1812.5$>\frac{725}{3}$,
∴网店试营销期间,第1天获得的利润最大,最大利润是1812.5元.
点评 本题考查二次函数的应用,解题的关键是明确题意可以分别求出函数的解析式,并且可以求函数的最值.

 如图,已知反比例函数的图象y=$\frac{k}{x}$(x<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-6,4).求:
如图,已知反比例函数的图象y=$\frac{k}{x}$(x<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-6,4).求: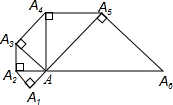 如上图,已知等腰Rt△AA1A2的直角边长为1,以Rt△AA1A2的斜边AA2为直角边,画第2个等腰Rt△AA2A3,再以Rt△AA2A3的斜边AA3为直角边,画第3个等腰Rt△AA3A4,…,依此类推直到第100个等腰Rt△AA100A101,则由这100个等腰直角三角形所构成的图形的面积为299-$\frac{1}{2}$.
如上图,已知等腰Rt△AA1A2的直角边长为1,以Rt△AA1A2的斜边AA2为直角边,画第2个等腰Rt△AA2A3,再以Rt△AA2A3的斜边AA3为直角边,画第3个等腰Rt△AA3A4,…,依此类推直到第100个等腰Rt△AA100A101,则由这100个等腰直角三角形所构成的图形的面积为299-$\frac{1}{2}$.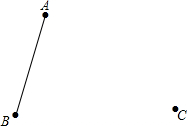 如图,已知三个点A,B,C.按要求完成下列问题:
如图,已知三个点A,B,C.按要求完成下列问题: