题目内容
7.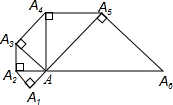 如上图,已知等腰Rt△AA1A2的直角边长为1,以Rt△AA1A2的斜边AA2为直角边,画第2个等腰Rt△AA2A3,再以Rt△AA2A3的斜边AA3为直角边,画第3个等腰Rt△AA3A4,…,依此类推直到第100个等腰Rt△AA100A101,则由这100个等腰直角三角形所构成的图形的面积为299-$\frac{1}{2}$.
如上图,已知等腰Rt△AA1A2的直角边长为1,以Rt△AA1A2的斜边AA2为直角边,画第2个等腰Rt△AA2A3,再以Rt△AA2A3的斜边AA3为直角边,画第3个等腰Rt△AA3A4,…,依此类推直到第100个等腰Rt△AA100A101,则由这100个等腰直角三角形所构成的图形的面积为299-$\frac{1}{2}$.
分析 根据等腰直角三角形的性质和勾股定理分别求出前三个直角三角形的面积,根据规律计算即可.
解答 解:∵等腰Rt△AA1A2的直角边长为1,
∴Rt△AA1A2的面积为$\frac{1}{2}$,AA2=$\sqrt{2}$,
∴Rt△AA2A3的面积为1,AA3=2,
∴Rt△AA3A4的面积为2,
∴由这100个等腰直角三角形所构成的图形的面积=$\frac{1}{2}$+1+2+4+8+…+298=299-$\frac{1}{2}$.
故答案为:299-$\frac{1}{2}$.
点评 本题考查的是等腰直角三角形的性质,掌握等腰直角三角形的两条直角边相等和勾股定理的应用是解题的关键.

练习册系列答案
相关题目
12. 如图,数一数,图中共有线段( )
如图,数一数,图中共有线段( )
 如图,数一数,图中共有线段( )
如图,数一数,图中共有线段( )| A. | 5条 | B. | 6条 | C. | 7条 | D. | 8条 |
16.已知关于x的方程$\frac{x-4}{x-3}$-m-4=$\frac{m}{3-x}$无解,则m的值是( )
| A. | m=-3 | B. | m=1 | C. | m=-3或1 | D. | m=1或3 |
17.下列算式中,运算结果为负数的是( )
| A. | -(-2) | B. | |-2| | C. | (-2)3 | D. | (-2)2 |
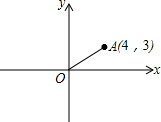 如图,在平面直角坐标系中,已知点A的坐标为(4,3),P是x轴上的一点,若以O,A,P三点组成的三角形为等腰三角形,则满足条件的点P共有4个.
如图,在平面直角坐标系中,已知点A的坐标为(4,3),P是x轴上的一点,若以O,A,P三点组成的三角形为等腰三角形,则满足条件的点P共有4个.