题目内容
12.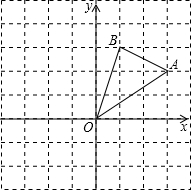 如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为(3,2)、(1,3).
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为(3,2)、(1,3).(1)M为点A关于O点中心对称的点,将△OAB平移得到△O1A1B1,使得O1点与点M重合,请在图中画出△O1A1B1,并直接写出点M的坐标为(-3,-2);
(2)将△AOB绕点O逆时针旋转90°后得到△OA2B2,请在图中画出△OA2B2,并直接写出点A2的坐标为(-2,3);
(3)请直接写出四边形OB1B2M的面积为5.
分析 (1)先利用关于原点对称的点的坐标特征得到M(-3,-2),则点O1平移到点M要先向下平移2个单位,再向左平移3个单位,利用此平移规律作出点B和点A的对应点即可;
(2)利用网格特点和旋转的性质作出点A和B的对应点A2和B2即可;
(3)把四边形OB1B2M化为两个三角形,然后根据三角形面积公式进行计算.
解答  解:(1)M点的坐标为(-3,-2),如图,△O1A1B1为所求;
解:(1)M点的坐标为(-3,-2),如图,△O1A1B1为所求;
(2)点A2的坐标为(-2,3),如图,△OA2B2为所求;
(3)四边形OB1B2M的面积=S△OB2M+S△OB1B2=$\frac{1}{2}$×(1+2)×3+$\frac{1}{2}$×1×1=5.
故答案为(-3,-2);(-2,3);(5.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
7.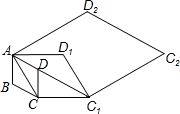 如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )
如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )
 如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )
如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )| A. | $\frac{\sqrt{3}}{2}$×3n | B. | $\frac{\sqrt{3}}{2}$×3n+1 | C. | $\frac{\sqrt{3}}{2}$×3n-1 | D. | $\frac{\sqrt{3}}{2}$×32n-1 |
4.小美将某服饰店的促销活动内容告诉小明后,小明假设某一商品的定价为x元,并列出关系式为0.3(2x-100)<1000,则下列何者可能是小美告诉小明的内容?( )
| A. | 买两件等值的商品可减100元,再打3折,最后不到1000元 | |
| B. | 买两件等值的商品可减100元,再打7折,最后不到1000元 | |
| C. | 买两件等值的商品可打3折,再减100元,最后不到1000元 | |
| D. | 买两件等值的商品可打7折,再减100元,最后不到1000元 |
1.等边三角形的边心距、半径、边长之比为( )
| A. | 1:$\sqrt{3}$:2 | B. | 1:2:$\sqrt{3}$ | C. | 1:2$\sqrt{3}$:2 | D. | 1:2:2$\sqrt{3}$ |
 如图,已知:A、F、C、D四点在一条直线上,AF=CD,BC=EF,且AB=DE. 请说明△ABC≌△DEF.
如图,已知:A、F、C、D四点在一条直线上,AF=CD,BC=EF,且AB=DE. 请说明△ABC≌△DEF.