题目内容
12.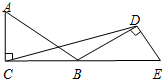 如图,△ABC绕着顶点B顺时针旋转150°得△EBD,连结CD,若∠ACB=90°,∠ABC=30°,则∠BDC的度数是15°.
如图,△ABC绕着顶点B顺时针旋转150°得△EBD,连结CD,若∠ACB=90°,∠ABC=30°,则∠BDC的度数是15°.
分析 根据旋转的性质得到BD=CB,由等腰三角形的性质得到∠DCB=∠BDC,根据三角形的外角的性质即可得到结论.
解答 解:∵△ABC绕着顶点B顺时针旋转150°得△EBD,
∴BD=CB,
∴∠DCB=∠BDC
又∵∠DBE=∠ABC=30°,∠DBE=∠DCB+∠BDC
故∠BDC=$\frac{1}{2}$∠DBE=15°,
故答案为:15°.
点评 本题考查了旋转的性质,等腰三角形的性质,熟练掌握旋转的性质是解题的关键.

练习册系列答案
相关题目
6.下列图形(如图所示)经过折叠不能围成正方体的是( )
| A. |  | B. |  | C. |  | D. |  |
1. 如图,利用直尺和三角尺作平行线,其依据是( )
如图,利用直尺和三角尺作平行线,其依据是( )
 如图,利用直尺和三角尺作平行线,其依据是( )
如图,利用直尺和三角尺作平行线,其依据是( )| A. | 同位角相等,两直线平行 | B. | 内错角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 两直线平行,同位角相等 |
2.已知|a+1|+$\sqrt{7+b}$=0,则a+b=( )
| A. | -8 | B. | -6 | C. | 6 | D. | 8 |
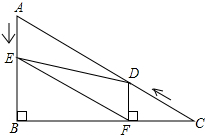 如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.