题目内容
17．当a=3时，化简（1+$\frac{1}{a-1}$）÷$\frac{a}{{a}^{2}-2a+1}$的结果是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 首先计算括号内的式子，把分式的除法转化为乘法，进行约分即可化简，然后代入数值计算即可．
解答 解：原式=$\frac{a}{a-1}$÷$\frac{a}{（a-1）^{2}}$
=$\frac{a}{a-1}$•$\frac{（a-1）^{2}}{a}$
=a-1，
当a=3时，原式=3-1=2．
故选B．
点评 本题考查了分式的混合运算，分式的混合运算，要注意运算顺序，式与数有相同的混合运算顺序；先乘方，再乘除，然后加减，有括号的先算括号里面的．最后结果分子、分母要进行约分，注意运算的结果要化成最简分式或整式．
练习册系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
×3
＝6
B. 
＋
＝
－2
＝3
D. 
÷
＝
5．下列方程组中，是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}{3{x}^{2}+y=1}\\{10x-8y=-9}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x-y=2}\\{\frac{1}{x}-3y=-\frac{7}{4}}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x=1}\\{2x-y=6}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{xy=4}\\{x+2y=6}\end{array}\right.$ |
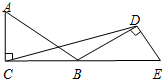如图，△ABC绕着顶点B顺时针旋转150°得△EBD，连结CD，若∠ACB=90°，∠ABC=30°，则∠BDC的度数是15°．
如图，⊙O的半径为6，AB是⊙O的弦，将线段BA绕点A逆时针旋转90°得到线段CA，当点A固定，点B在圆上运动时，则线段OC长度的最小值为6$\sqrt{2}$-6．
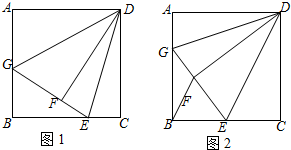
某市有A、B、C、D四个大型超市，分别位于一条东西走向的平安大路两侧，如图，若C（-2，8）、D（0，0），请建立适当的直角坐标系，并写出A、B两个超市相应的坐标．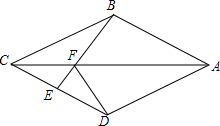
如图，在四边形ABCD中，AB=AD，CB=CD，E是CD上一点，BE交AC于F，连接DF．