题目内容
16.如图,二次函数y=x2+px+q(p<0)的图象与x轴交于A、B两点,与y轴交于点C(0,-1),△ABC的面积为$\frac{5}{4}$.(1)求A、B两点的坐标和该二次函数的关系式;
(2)过y轴上的一点M(0,m)作y轴的垂线,若该垂线与△ABC的外接圆有公共点,求m的取值范围;
(3)在该二次函数的图象上是否存在点D,使以A、B、C、D为顶点的四边形为直角梯形?若存在,求出点D的坐标;若不存在,请说明理由.

分析 (1)由与y轴交于点C(0,-1),△ABC的面积为$\frac{5}{4}$,可求得AB的长,然后设点A的坐标为(a,0),利用交点式抛物线得解析式y=(x-a)(x-a-$\frac{5}{2}$),再把点C(0,-1)代入即可求得答案;
(2)由(1)易证得△AOC∽△COB,即可得△ABC是以AB为斜边的直角三角形,外接圆的直径为AB,继而求得答案;
(3)分别从AD∥BC与BD∥AC,去分析求解即可求得答案.
解答 解:(1)∵OC=1,△ABC的面积为$\frac{5}{4}$,
∴AB=$\frac{5}{2}$.
设点A的坐标为(a,0),那么点B的坐标为(a+$\frac{5}{2}$,0).
设抛物线的解析式为:y=(x-a)(x-a-$\frac{5}{2}$),
代入点C(0,-1),得a(a+$\frac{5}{2}$)=-1.
解得:a=-$\frac{1}{2}$或a=-2.
∵二次函数的解析式y=x2+px+q中,p<0,
∴抛物线的对称轴在y轴右侧.
∴点A、B的坐标分别为(-$\frac{1}{2}$,0),(2,0).
∴抛物线的解析式为y=(x+$\frac{1}{2}$)(x-2)=x2-$\frac{3}{2}$x-1.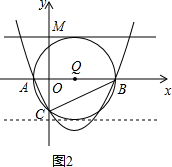 (2)如图2,∵OA•OB=1,OC2=1,
(2)如图2,∵OA•OB=1,OC2=1,
∴$\frac{OA}{OC}=\frac{OC}{OB}$,
∵∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴∠ACO=∠OBC,
∵∠OBC+∠OCB=90°,
∴∠ACB=∠ACO+∠OCB=90°,
∴△ABC是以AB为斜边的直角三角形,外接圆的直径为AB.
∴m的取值范围是-$\frac{5}{4}$≤m≤$\frac{5}{4}$.
(3)设点D的坐标为(x,(x+$\frac{1}{2}$)(x-2)).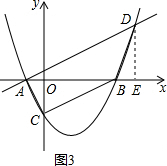
①如图3,过点A作BC的平行线交抛物线于D,过点D作DE⊥x轴于E.
∵tan∠DAB=tan∠OBC,
∴$\frac{DE}{AE}=\frac{OC}{OB}$=$\frac{1}{2}$.
∴$\frac{(x+\frac{1}{2})(x-2)}{x+\frac{1}{2}}$=$\frac{1}{2}$.
解得x=$\frac{5}{2}$.
此时点D的坐标为($\frac{5}{2}$,$\frac{3}{2}$).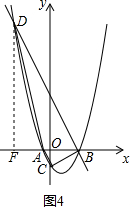 过点B作AC的平行线交抛物线于D,过点D作DF⊥x轴于F.
过点B作AC的平行线交抛物线于D,过点D作DF⊥x轴于F.
∵tan∠DBF=tan∠CAO,
∴$\frac{DF}{BF}=\frac{OC}{OA}$=2,
∴$\frac{(x+\frac{1}{2})(x-2)}{2-x}$=2.
解得x=-$\frac{5}{2}$.
此时点D的坐标为(-$\frac{5}{2}$,9).
综上所述,当D的坐标为($\frac{5}{2}$,$\frac{3}{2}$)或(-$\frac{5}{2}$,9)时,以A、B、C、D为顶点的四边形为直角梯形.
点评 此题属于二次函数的综合题,考查了待定系数求函数解析式、相似三角形的判定与性质、圆周角定理以及三角函数等知识.注意分类讨论思想与方程思想的应用是解此题的关键.

| A. | 2$\sqrt{5}$ | B. | 2π | C. | 6π | D. | 3$\sqrt{5}$π |
| A. |  | B. |  | C. |  | D. |  |
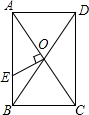 如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则AE=5.
如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则AE=5.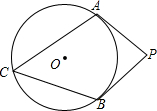 如图,PA、PB是⊙O的两条切线,点C在⊙O上,若∠APB=80°,则∠ACB=50度.
如图,PA、PB是⊙O的两条切线,点C在⊙O上,若∠APB=80°,则∠ACB=50度.