题目内容
 如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合,AD=1,AE=
如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合,AD=1,AE=| 1 |
| 3 |
考点:旋转的性质
专题:计算题
分析:先利用勾股定理计算出DE=
,再根据旋转的性质得DF=DE,∠FDE=∠CDA=90°,则可判断△DEF为等腰直角三角形,所以EF=
DE,然后把DE的长代入计算即可.
| ||
| 3 |
| 2 |
解答: 解:连接EF,如图,
解:连接EF,如图,
在Rt△ADE中,∵AD=1,AE=
,
∴DE=
=
,
∵F为BC边的延长线上一点,△DAE旋转后能与△DCF重合,
∴DF=DE,∠FDE=∠CDA=90°,
∴△DEF为等腰直角三角形,
∴EF=
DE=
•
=
.
 解:连接EF,如图,
解:连接EF,如图,在Rt△ADE中,∵AD=1,AE=
| 1 |
| 3 |
∴DE=
| AD2+AE2 |
| ||
| 3 |
∵F为BC边的延长线上一点,△DAE旋转后能与△DCF重合,
∴DF=DE,∠FDE=∠CDA=90°,
∴△DEF为等腰直角三角形,
∴EF=
| 2 |
| ||
| 3 |
| 2 |
2
| ||
| 3 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是( )
①平行四边形;②菱形;③矩形;④对角线互相垂直的四边形.
①平行四边形;②菱形;③矩形;④对角线互相垂直的四边形.
| A、①③ | B、②③ | C、③④ | D、②④ |
响水县实验初中的校园面积约是102000平方米,用科学记数法表示为( )
| A、102×103 |
| B、10.2×104 |
| C、1.02×105 |
| D、0.102×106 |
等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,则连续翻转2015次后,点A( )
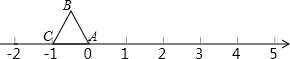
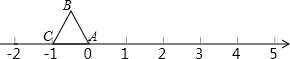
| A、不对应任何数 |
| B、对应的数是2013 |
| C、对应的数是2014 |
| D、对应的数是2015 |
二次函数y=-x2+2x的图象可能是( )
A、 |
B、 |
C、 |
D、 |
 一个几何体是由几个大小相同的小正方体摆成,如图是该几何体从上面和从左面看到的几何体的直观图,请你画出这个几何体从前面看到的图形.(画出所有可能情况)
一个几何体是由几个大小相同的小正方体摆成,如图是该几何体从上面和从左面看到的几何体的直观图,请你画出这个几何体从前面看到的图形.(画出所有可能情况)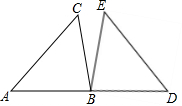 在△ABC中,∠A=45°,∠B=75°,BC=2,将Rt△ABC绕点B旋转至△BDE的位置,如图所示,且使A、B、D在同一条直线上,请在图中表示出AC边扫过的图形,并计算其面积.
在△ABC中,∠A=45°,∠B=75°,BC=2,将Rt△ABC绕点B旋转至△BDE的位置,如图所示,且使A、B、D在同一条直线上,请在图中表示出AC边扫过的图形,并计算其面积.