题目内容
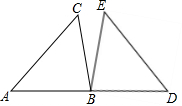 在△ABC中,∠A=45°,∠B=75°,BC=2,将Rt△ABC绕点B旋转至△BDE的位置,如图所示,且使A、B、D在同一条直线上,请在图中表示出AC边扫过的图形,并计算其面积.
在△ABC中,∠A=45°,∠B=75°,BC=2,将Rt△ABC绕点B旋转至△BDE的位置,如图所示,且使A、B、D在同一条直线上,请在图中表示出AC边扫过的图形,并计算其面积.考点:旋转的性质,扇形面积的计算
专题:计算题
分析:作BG⊥AC于G,BH⊥DE于H,如图,则点G为线段AB上离B点最近的点,再分别作出点A、点G、点C旋转时的路径,即对应的弧,由此得到AC边扫过的图形分两部分:第一部分为线段AC、弧CM、线段ME和弧AE所围长成的图形;第二部分为线段GC、弧GH、线段HD和弧DC所围成的图形,再利用解直角三角形得到
AB=
,BG=
,AC=
+1,接着利用旋转的性质得到∠EBD=∠ABC=75°,则∠CBM=30°,然后根据扇形面积公式和利用面积的和差分别计算两部分的面积,再把它们相加即可.
AB=
| 6 |
| 3 |
| 3 |
解答: 解:作BG⊥AC于G,BH⊥DE于H,如图,
解:作BG⊥AC于G,BH⊥DE于H,如图,
AC边扫过的图形分两部分:第一部分为线段AC、弧CM、线段ME和弧AE所围长成的图形;第二部分为
线段GC、弧GH、线段HD和弧DC所围成的图形.
∵∠A=45°,∠B=75°,
∴∠ACB=60°,
在Rt△BCG中,CG=
BC=1,BG=
CG=
,
在Rt△ABG中,AG=BG=
,AB=
BG=
,
∴AC=AG+GC=
+1,
∵Rt△ABC绕点B旋转至△EBD的位置,
∴∠EBD=∠ABC=75°,
∵A、B、D在同一条直线上,
∴∠CBM=180°-2×75°=30°,
线段AC、弧CM、线段ME和弧AE所围长成的图形的面积=S扇形ABE-S△ABC-S扇形CBM
=
-
•
•(
+1)-
=
π-
,
线段GC、弧GH、线段HD和弧DC所围成的图形的面积=S扇形CBD-S扇形PBN
=
-
=
,
∴AC边扫过的图形的面积=
π-
+
π=
π-
-
.
 解:作BG⊥AC于G,BH⊥DE于H,如图,
解:作BG⊥AC于G,BH⊥DE于H,如图,AC边扫过的图形分两部分:第一部分为线段AC、弧CM、线段ME和弧AE所围长成的图形;第二部分为
线段GC、弧GH、线段HD和弧DC所围成的图形.
∵∠A=45°,∠B=75°,
∴∠ACB=60°,
在Rt△BCG中,CG=
| 1 |
| 2 |
| 3 |
| 3 |
在Rt△ABG中,AG=BG=
| 3 |
| 2 |
| 6 |
∴AC=AG+GC=
| 3 |
∵Rt△ABC绕点B旋转至△EBD的位置,
∴∠EBD=∠ABC=75°,
∵A、B、D在同一条直线上,
∴∠CBM=180°-2×75°=30°,
线段AC、弧CM、线段ME和弧AE所围长成的图形的面积=S扇形ABE-S△ABC-S扇形CBM
=
105•π•(
| ||
| 360 |
| 1 |
| 2 |
| 3 |
| 3 |
| 30π•22 |
| 360 |
=
| 17 |
| 12 |
3+
| ||
| 2 |
线段GC、弧GH、线段HD和弧DC所围成的图形的面积=S扇形CBD-S扇形PBN
=
| 105•π•22 |
| 360 |
105•π•(
| ||
| 360 |
=
| 7π |
| 24 |
∴AC边扫过的图形的面积=
| 17 |
| 12 |
3+
| ||
| 2 |
| 7 |
| 24 |
| 41 |
| 24 |
| 3 |
| 2 |
| ||
| 2 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了扇形面积的计算.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合,AD=1,AE=
如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合,AD=1,AE=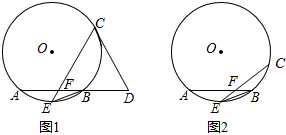
 如图,三个皮带轮的半径都是10dm,中心距离BC=30dm,AC=40dm,AB=50dm,求皮带的长度.
如图,三个皮带轮的半径都是10dm,中心距离BC=30dm,AC=40dm,AB=50dm,求皮带的长度.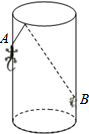 如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,求壁虎捕捉蚊子的最短距离.(容器厚度忽略不计)
如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,求壁虎捕捉蚊子的最短距离.(容器厚度忽略不计)