题目内容
顺次连接一个四边形的各边中点，得到了一个矩形，则下列四边形中满足条件的是（ ）
①平行四边形；②菱形；③矩形；④对角线互相垂直的四边形．
①平行四边形；②菱形；③矩形；④对角线互相垂直的四边形．
| A、①③ | B、②③ | C、③④ | D、②④ |
考点：中点四边形
专题：
分析：有一个角是直角的平行四边形是矩形，根据此可知顺次连接对角线垂直的四边形是矩形．
解答：
解：AC⊥BD，E，F，G，H是AB，BC，CD，DA的中点，
∵EH∥BD，FG∥BD，
∴EH∥FG，
同理；EF∥HG，
∴四边形EFGH是平行四边形．
∵AC⊥BD，
∴EH⊥EF，
∴四边形EFGH是矩形．
所以顺次连接对角线垂直的四边形是矩形．
而菱形、正方形的对角线互相垂直，则菱形、正方形均符合题意．
故选：D．
解：AC⊥BD，E，F，G，H是AB，BC，CD，DA的中点，∵EH∥BD，FG∥BD，
∴EH∥FG，
同理；EF∥HG，
∴四边形EFGH是平行四边形．
∵AC⊥BD，
∴EH⊥EF，
∴四边形EFGH是矩形．
所以顺次连接对角线垂直的四边形是矩形．
而菱形、正方形的对角线互相垂直，则菱形、正方形均符合题意．
故选：D．
点评：本题考查矩形的判定定理和三角形的中位线的定理，从而可求解．
练习册系列答案
名校课堂系列答案
相关题目
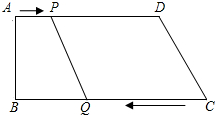如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AB=8厘米，AD=24厘米，BC=26厘米，动点P从点A开始沿AD边向点D以1厘米/秒的速度运动，动点Q从点C开始沿CB边向点B以3厘米/秒的速度运动，P、Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒．问：如图，该图形的相邻两边均互相垂直，则这个图形的周长为（ ）
| A、37 | B、26 | C、42 | D、21 |
如图，△ABC中，AB=AC，∠A=30°，AB的垂直平分线MN交AC于D，则∠DBC的度数为（ ）| A、60° | B、45° |
| C、40° | D、30° |
若分式
有意义，则（ ）
| 2 |
| x-1 |
| A、x＞1 | B、x≠1 |
| C、x≥1 | D、x=1 |
如图，E为正方形ABCD的边AB上一点（不含A、B点），F为BC边的延长线上一点，△DAE旋转后能与△DCF重合，AD=1，AE=