题目内容
若一个多边形的外角和是其内角和的
,则此多边形的边数为 .
| 2 |
| 5 |
考点:多边形内角与外角
专题:计算题
分析:设这个多边形的边数为n,再根据多边形内角和定理和外角和等于360度得到
(n-2)•180°=360°,然后解方程即可.
| 2 |
| 5 |
解答:解:设这个多边形的边数为n,
根据题意得
(n-2)•180°=360°,
所以n=7.
故答案为7.
根据题意得
| 2 |
| 5 |
所以n=7.
故答案为7.
点评:本题考查了多边形内角与外角:多边形内角和定理:(n-2)•180°(n≥3)且n为整数);多边形的外角和等于360度.

练习册系列答案
相关题目
下列说法正确的是( )
| A、对角线相等且互相平分的四边形是菱形 |
| B、对角线相等且互相垂直的四边形是菱形 |
| C、对角线相等且互相平分的四边形是矩形 |
| D、对角线相等且垂直的四边形是正方形 |
 如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合,AD=1,AE=
如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合,AD=1,AE= 如图,三个皮带轮的半径都是10dm,中心距离BC=30dm,AC=40dm,AB=50dm,求皮带的长度.
如图,三个皮带轮的半径都是10dm,中心距离BC=30dm,AC=40dm,AB=50dm,求皮带的长度.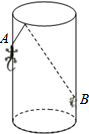 如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,求壁虎捕捉蚊子的最短距离.(容器厚度忽略不计)
如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,求壁虎捕捉蚊子的最短距离.(容器厚度忽略不计) 如图,已知AB∥DE,AB=DE,请你添加一个条件
如图,已知AB∥DE,AB=DE,请你添加一个条件