题目内容
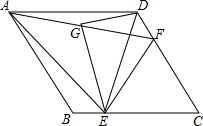 如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,∠DAE=∠BAF.
如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,∠DAE=∠BAF. (1)求证:CE=CF;
(2)若∠ABC=120°,点G是线段AF的中点,连接DG,EG.求证:DG⊥GE.
考点:菱形的性质,全等三角形的判定与性质
专题:证明题
分析:(1)欲证明CE=CF,只需证得BE=DF,所以利用全等三角形△ABE≌△ADF的性质来推知BE=DF即可;
(2)如图,延长EG到点H,使HG=EG,连接HA、HD.构建全等三角形△HAG≌△EFG、△HAD≌△ECD、△DGH≌△DGE,利用全等三角形的对应角相等来证明∠DGH=∠DGE=90°,即DG⊥GE.
(2)如图,延长EG到点H,使HG=EG,连接HA、HD.构建全等三角形△HAG≌△EFG、△HAD≌△ECD、△DGH≌△DGE,利用全等三角形的对应角相等来证明∠DGH=∠DGE=90°,即DG⊥GE.
解答: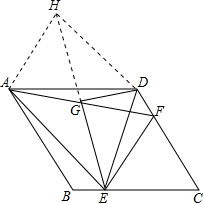 证明:(1)∵四边形ABCD是菱形,
证明:(1)∵四边形ABCD是菱形,
∴AB=AD=DC=BC.
∵∠DAE=∠BAF,
∴∠BAE=∠DAF.
在△ABE与△ADF中,
,
∴△ABE≌△ADF(SAS),
∴BE=DF,
∴BC-BE=DC-DF,即CE=CF;
(2)如图,延长EG到点H,使HG=EG,连接HA、HD.
∵点G是AF的中点,
∴AG=FG,
在△HAG与△EFG中,
,
∴△HAG≌△EFG(SAS),
∴EF=AH,∠HAG=∠EFG,
∴AH∥EF.
∵四边形ABCD是菱形,
∴DC=BC=AD.
∵由(1)知,BE=DF,且∠BAE=∠DAF,EC=FC.
∵∠ABC=120°,
∴∠C=60°,
∴△EFC是等边三角形,
∴∠FEC=60°,
∴EC=FE.
由上述知,FE=HA,
∴EC=HA,∠HAG=∠HAD+∠DAF=∠EFG.
∵AF=AE,
∴∠FEF=∠AEF.
∵∠BAD=60°,
∴∠EAF=60°-∠BAE-∠DAF=60°-2∠DAF.
在△AEF中,∠EAF=108°-∠AEF-∠EFG=180°-2∠EFG=180°-2(∠HAD+∠DAF),
∴∠HAD=60°.
在△HAD与△ECD中,
,
∴△HAD≌△ECD(SAS),
∴DE=DH,
易证△DGH≌△DGE,
故∠DGH=∠DGE=90°,即DG⊥GE.
 证明:(1)∵四边形ABCD是菱形,
证明:(1)∵四边形ABCD是菱形,∴AB=AD=DC=BC.
∵∠DAE=∠BAF,
∴∠BAE=∠DAF.
在△ABE与△ADF中,
|
∴△ABE≌△ADF(SAS),
∴BE=DF,
∴BC-BE=DC-DF,即CE=CF;
(2)如图,延长EG到点H,使HG=EG,连接HA、HD.
∵点G是AF的中点,
∴AG=FG,
在△HAG与△EFG中,
|
∴△HAG≌△EFG(SAS),
∴EF=AH,∠HAG=∠EFG,
∴AH∥EF.
∵四边形ABCD是菱形,
∴DC=BC=AD.
∵由(1)知,BE=DF,且∠BAE=∠DAF,EC=FC.
∵∠ABC=120°,
∴∠C=60°,
∴△EFC是等边三角形,
∴∠FEC=60°,
∴EC=FE.
由上述知,FE=HA,
∴EC=HA,∠HAG=∠HAD+∠DAF=∠EFG.
∵AF=AE,
∴∠FEF=∠AEF.
∵∠BAD=60°,
∴∠EAF=60°-∠BAE-∠DAF=60°-2∠DAF.
在△AEF中,∠EAF=108°-∠AEF-∠EFG=180°-2∠EFG=180°-2(∠HAD+∠DAF),
∴∠HAD=60°.
在△HAD与△ECD中,
|
∴△HAD≌△ECD(SAS),
∴DE=DH,
易证△DGH≌△DGE,
故∠DGH=∠DGE=90°,即DG⊥GE.
点评:本题考查了菱形的性质的运用,线段的中点的性质的运用,全等三角形的判定及性质的运用,解答时运用菱形的性质证明三角形全等是关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
将3180000元用科学记数法表示为( )
| A、0.318×107元 |
| B、3.18×106元 |
| C、31.8×105元 |
| D、318×104元 |
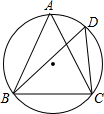 如图,在⊙O中,
如图,在⊙O中, |
| AB |
 |
| AC |
(1)求证:△ABC是等边三角形.
(2)过点B作BP∥CD,交DA延长线于点P,请依题意画出示意图.若AD=1,CD=5,求BD的长.
有统计数据显示,2014年中国人在餐桌上浪费的粮食价值高达2000亿元,被倒掉的实物相当于2亿多人一年的口粮,所以我们要“注意节约,拒绝舌尖上的浪费”.2000亿这个数用科学记数法表示为( )
| A、2000×108 |
| B、2×1011 |
| C、0.2×1012 |
| D、20×1010 |
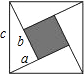 如图,由4个边长为a,b,c的直角三角形拼成一个正方形,中间有一个小正方形的开口(图中阴影部分),试用不同的方法计算这个阴影部分的面积,你发现了什么?
如图,由4个边长为a,b,c的直角三角形拼成一个正方形,中间有一个小正方形的开口(图中阴影部分),试用不同的方法计算这个阴影部分的面积,你发现了什么?