题目内容
 如图,点P从点A出发沿着线段AB向点B匀速运动,点P出发4分钟时距A地240cm,此时点Q也从点A沿着线段AB向点B匀速运动,再经过6分钟点Q追上点P,又经过2分钟点Q到达点B处,此时点P、Q同时停止运动,设点P的运动时间为t分钟.
如图,点P从点A出发沿着线段AB向点B匀速运动,点P出发4分钟时距A地240cm,此时点Q也从点A沿着线段AB向点B匀速运动,再经过6分钟点Q追上点P,又经过2分钟点Q到达点B处,此时点P、Q同时停止运动,设点P的运动时间为t分钟.(1)求点A到点B的距离;
(2)当线段PQ的长为40cm时,求t的值.
考点:一元一次方程的应用,两点间的距离
专题:
分析:(1)由点P出发4分钟时距A地240cm,可得点P的运动速度是每分钟60cm,设点Q的运动速度是每分钟xcm,根据经过6分钟点Q追上点P列出方程,解方程求出x的值,进而得到点A到点B的距离;
(2)分两种情况:①P在Q前面;②P在Q后面;根据线段PQ的长为40cm,列出方程求解即可.
(2)分两种情况:①P在Q前面;②P在Q后面;根据线段PQ的长为40cm,列出方程求解即可.
解答:解:(1)∵点P出发4分钟时距A地240cm,
∴点P的运动速度是每分钟60cm.
设点Q的运动速度是每分钟xcm,根据题意得
6x=240+6×60,
解得x=100,
则点A到点B的距离为:100×(6+2)=800(cm).
答:点A到点B的距离为800cm;
(2)①P在Q前面,依题意有
60t-100(t-4)=40,
解得t=9;
②P在Q后面,依题意有
100(t-4)-60t=40,
解得t=11.
答:t的值是9分钟或11分钟.
∴点P的运动速度是每分钟60cm.
设点Q的运动速度是每分钟xcm,根据题意得
6x=240+6×60,
解得x=100,
则点A到点B的距离为:100×(6+2)=800(cm).
答:点A到点B的距离为800cm;
(2)①P在Q前面,依题意有
60t-100(t-4)=40,
解得t=9;
②P在Q后面,依题意有
100(t-4)-60t=40,
解得t=11.
答:t的值是9分钟或11分钟.
点评:本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.注意分类思想的应用.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
有统计数据显示,2014年中国人在餐桌上浪费的粮食价值高达2000亿元,被倒掉的实物相当于2亿多人一年的口粮,所以我们要“注意节约,拒绝舌尖上的浪费”.2000亿这个数用科学记数法表示为( )
| A、2000×108 |
| B、2×1011 |
| C、0.2×1012 |
| D、20×1010 |
若菱形ABCD的对角线AC、BD交于点O,且AC=16,BD=12,则菱形的边长为( )
| A、10 | B、12 | C、28 | D、40 |
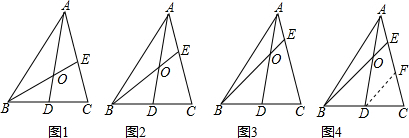
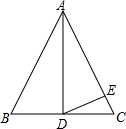 如图,△ABC中,AB=AC,点D是BC的中点,E是AC上一点,且AE=AD,若∠AED=75°,则∠EDC的度数是
如图,△ABC中,AB=AC,点D是BC的中点,E是AC上一点,且AE=AD,若∠AED=75°,则∠EDC的度数是 如图所示的是一块从一边长为50cm的正方形材料中裁出的垫片,现测得FG=9cm,求这块垫片的周长.
如图所示的是一块从一边长为50cm的正方形材料中裁出的垫片,现测得FG=9cm,求这块垫片的周长.