题目内容
1.△ABC的三边a、b、c满足|a+b-50|+$\sqrt{a-b-32}$+(c-40)2=0.试判断△ABC的形状是直角三角形.分析 先利用非负数的性质,分别求出a、b、c的值,然后利用勾股定理的逆定理证明△ABC是直角三角形.
解答 解:∵|a+b-50|+$\sqrt{a-b-32}$+(c-40)2=0,
∴$\left\{\begin{array}{l}{a+b-50=0}\\{a-b-32=0}\\{c-40=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=41}\\{b=9}\\{c=40}\end{array}\right.$,
∵92+402=412,
∴△ABC是直角三角形.
故答案为直角三角形.
点评 此题主要考查了勾股定理的逆定理以及绝对值、偶次方和算术平方根的性质,得出a、b、c的值是解题关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
11.若分式$\frac{2x-y}{y}$中的x,y的值变为原来的2倍,则此分式的值( )
| A. | 不变 | B. | 发生变化 | C. | 是原来的2倍 | D. | 是原来的$\frac{1}{2}$ |
11.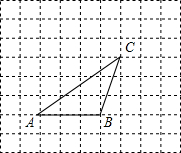 在正方形网格中,△ABC的位置如图所示,则sin∠BAC的值为( )
在正方形网格中,△ABC的位置如图所示,则sin∠BAC的值为( )
 在正方形网格中,△ABC的位置如图所示,则sin∠BAC的值为( )
在正方形网格中,△ABC的位置如图所示,则sin∠BAC的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
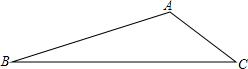 △ABC是武汉市在拆除违章建筑后的一块三角形空地,已知∠A=150°,AB=30m,AC=20m,如果要在这块空地上种草皮,按每平方米a元计算,则需要资金多少元?
△ABC是武汉市在拆除违章建筑后的一块三角形空地,已知∠A=150°,AB=30m,AC=20m,如果要在这块空地上种草皮,按每平方米a元计算,则需要资金多少元?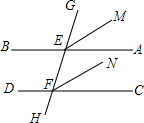 如图,直线AB,CD被直线GH所截,且∠AEG=∠CFG,EM,FN分别平分∠AEG和∠CFG.试说明EM∥FN.
如图,直线AB,CD被直线GH所截,且∠AEG=∠CFG,EM,FN分别平分∠AEG和∠CFG.试说明EM∥FN.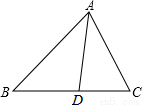 如图,△ABC中,AD是∠BAC的角平分线,AB=4,AC=3,则△ABD与△ADC的面积比是4:3.
如图,△ABC中,AD是∠BAC的角平分线,AB=4,AC=3,则△ABD与△ADC的面积比是4:3.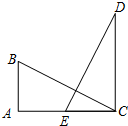 如图,AB⊥AC,垂足为A,CD⊥AC,垂足为C,DE⊥BC,且AB=CE,若BC=5cm,则DE的长为5cm.
如图,AB⊥AC,垂足为A,CD⊥AC,垂足为C,DE⊥BC,且AB=CE,若BC=5cm,则DE的长为5cm.