题目内容
16.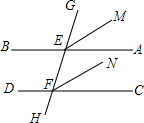 如图,直线AB,CD被直线GH所截,且∠AEG=∠CFG,EM,FN分别平分∠AEG和∠CFG.试说明EM∥FN.
如图,直线AB,CD被直线GH所截,且∠AEG=∠CFG,EM,FN分别平分∠AEG和∠CFG.试说明EM∥FN.
分析 由EM,FN分别平分∠AEG和∠CFG,可得∠GEM=$\frac{1}{2}$∠AEG,∠GFN=$\frac{1}{2}∠$CFG,然后由∠AEG=∠CFG,可得∠GEM=∠GFN,然后由同位角相等两直线平行即可说明EM∥FN.
解答 证明:∵EM,FN分别平分∠AEG和∠CFG,
∴∠GEM=$\frac{1}{2}$∠AEG,∠GFN=$\frac{1}{2}∠$CFG,
∵∠AEG=∠CFG,
∴∠GEM=∠GFN,
∴EM∥FN.
点评 此题考查了平行线的判定,解题的关键是:熟记同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行.

练习册系列答案
相关题目
7.代数式$\frac{1}{\sqrt{x-2}}$有意义的x取值范围是( )
| A. | x≥2 | B. | x>2 | C. | x≠2 | D. | x<2 |
4.(-0.5)2的平方根是( )
| A. | -0.5 | B. | ±0.5 | C. | 0.5 | D. | 0.25 |
11.在等式a3•a2•( )=a11中,括号里面的代数式是( )
| A. | a7 | B. | a8 | C. | a6 | D. | a3 |
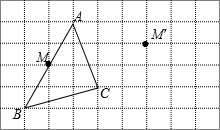 (1)如图,点M是△ABC中AB的中点,经平移后,点M落在M′处.请在正方形网格中画出△ABC平移后的图形△A′B′C′.
(1)如图,点M是△ABC中AB的中点,经平移后,点M落在M′处.请在正方形网格中画出△ABC平移后的图形△A′B′C′.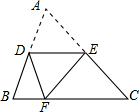 如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=65°,则∠BDF=50°.
如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=65°,则∠BDF=50°.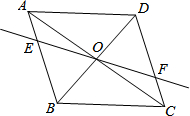 如图,在?ABCD中,对角线AC、BD交于点O,经过点O的直线交AB于E,交CD于F.
如图,在?ABCD中,对角线AC、BD交于点O,经过点O的直线交AB于E,交CD于F.