题目内容
13.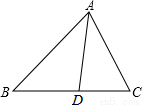 如图,△ABC中,AD是∠BAC的角平分线,AB=4,AC=3,则△ABD与△ADC的面积比是4:3.
如图,△ABC中,AD是∠BAC的角平分线,AB=4,AC=3,则△ABD与△ADC的面积比是4:3.
分析 根据角平分线上的点到角的两边距离相等可得点D到AB、AC的距离相等,再根据等高的三角形的面积的比等于底边的比求解.
解答 解:∵AD是∠BAC的角平分线,
∴点D到AB、AC的距离相等,
∴△ABD与△ADC的面积比=AB:AC=4:3.
故答案为:4:3.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,等高的三角形的面积的比等于底边的比,熟记性质与等高的三角形的面积的关系是解题的关键.

练习册系列答案
相关题目
4.(-0.5)2的平方根是( )
| A. | -0.5 | B. | ±0.5 | C. | 0.5 | D. | 0.25 |
3.下列命题中,不正确的是( )
| A. | 对角线相等的平行四边形是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 三角形的中位线平行于第三边且等于第三边的一半 | |
| D. | 三角形的一条中线能将三角形分成面积相等的两部分 |
 如图,MN∥BC,∠AEN=100°,∠B=65°,则∠A=35°.
如图,MN∥BC,∠AEN=100°,∠B=65°,则∠A=35°.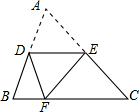 如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=65°,则∠BDF=50°.
如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=65°,则∠BDF=50°.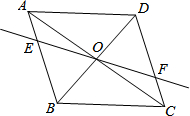 如图,在?ABCD中,对角线AC、BD交于点O,经过点O的直线交AB于E,交CD于F.
如图,在?ABCD中,对角线AC、BD交于点O,经过点O的直线交AB于E,交CD于F.