题目内容

6．已知$\left\{\begin{array}{l}{2x-y=1}\\{x+4y=3}\end{array}\right.$，则x+y=$\frac{4}{3}$．

分析 方程组中两方程相加即可求出x+y的值．

解答 解：$\left\{\begin{array}{l}{2x-y=1①}\\{x+4y=3②}\end{array}\right.$，
①+②得：3x+3y=4，
则x+y=$\frac{4}{3}$．
故答案为：$\frac{4}{3}$．

点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．

练习册系列答案
相关题目
16．下列多项式不是完全平方式的是（　　）
A．x2+4x+4B．$\frac{1}{4}$x2-x+1C．4x2+4x+1D．x2-2x+$\frac{1}{4}$
17．已知函数y=（5m-3）x2-n+m+n是y关于x的正比例函数，则m=-1，n=1．
14．如图，已知：在矩形ABCD中，O为AC的中点，直线l经过点B，且直线l绕着点B旋转，AM⊥l于点M，CN⊥l于点N，连接OM，ON
（1）当直线l经过点D时，如图1，则OM、ON的数量关系为OM=ON；
（2）当直线l与线段CD交于点F时，如图2（1）中的结论是否仍然成立？若成立，请加以证明；若不成立，请说明理由；
（3）当直线l与线段DC的延长线交于点P时，请在图3中作出符合条件的图形，并判断（1）中的结论是否仍然成立？不必说明理由．
1．△ABC的三边a、b、c满足|a+b-50|+$\sqrt{a-b-32}$+（c-40）2=0．试判断△ABC的形状是直角三角形．
11．一天，小明在玩纸片拼图游戏时，发现利用图①中的三种材料各若干，可以拼出一些长方形来解释某些等式，比如图②可以解释为等式：（a+2b）（a+b）=a2+3ab+2b2．
（1）则图③可以解释为等式：（a+2b）（2a+b）=2a2+2b2+5ab．
（2）如图④，把边长为a+b（a≠b）的大正方形分割成两个边长分别是a、b的小正方形及两个矩形，试比较两个小正方形的面积之和S1与两个矩形面积之和S2的大小．
（3）小明取其中的若干张拼成一个面积为a2+nab+2b2长方形，则n可取的正整数值为4或6，并请在图⑤位置画出拼成的图形．
18．关于x的一元一次方程$\frac{2x+a}{3}$=$\frac{1-x}{2}$的解是正数，则a的取值范围为a＜$\frac{3}{2}$．
15．若直角三角形的三边长分别为a-b、a、a+b，且a、b都是正整数，则三角形其中一边的长可能为（　　）
A．22B．32C．62D．82
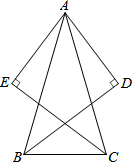16．如图，△ABC为等腰三角形，AB=AC，BD分别平分∠ABC，CE分别平分∠ACB，过点A分别作BD、CE的垂线段，垂足为D、E．求证：AD=AE．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网