题目内容
8.如图在给定的一张平行四边形纸片上作一个菱形,甲、乙两人的作法如下:甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠BAD,∠ABC的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法请分别做出判断,并证明.

分析 对于甲做法:利用MN垂直平分AC得到AO=CO,∠AOM=90°,再由AD∥BC得到∠MAC=∠NCA,则可证明△AOPM≌△CON,所以OM=ON,于是根据菱形的判定方法可判断四边形ANCM是菱形;
对于乙做法:由AE平分∠BAD得到∠BAE=∠EAF,再由AD∥BC得到∠EAF=∠BEA,则∠BAE=∠BEA,所以AB=BE,同理可得AB=AF,所以BE=AF,于是可证明四边形ABEF为平行四边形,再加上邻边相等可判断四边形ANCM是菱形.
解答 解:甲、乙做法都正确.
甲做法:
证明:∵MN垂直平分AC,
∴AO=CO,∠AOM=90°,
又∵AD∥BC,
∴∠MAC=∠NCA,
在△AOPM和△CON中,
$\left\{\begin{array}{l}{∠MAO=∠NCO}\\{OA=OC}\\{∠AOM=∠CON}\end{array}\right.$,
∴△AOPM≌△CON,
∴OM=ON,
∴AC和MN互相垂直平分,
∴四边形ANCM是菱形;
乙做法:
证明:∵AE平分∠BAD,
∴∠BAE=∠EAF,
又∵AD∥BC,
∴∠EAF=∠BEA,
∴∠BAE=∠BEA
∴AB=BE,
同理可得AB=AF,
∴BE=AF,
∵BE∥AF,
∴四边形ABEF为平行四边形
又∵AB=BE,
∴四边形ANCM是菱形.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了菱形的判定.

练习册系列答案
相关题目
13. 如图,一次函数y=kx+b的图象经过第一、二、三象限,若点A(1,2)在此图象上,则不等式kx+b>2的解集为( )
如图,一次函数y=kx+b的图象经过第一、二、三象限,若点A(1,2)在此图象上,则不等式kx+b>2的解集为( )
 如图,一次函数y=kx+b的图象经过第一、二、三象限,若点A(1,2)在此图象上,则不等式kx+b>2的解集为( )
如图,一次函数y=kx+b的图象经过第一、二、三象限,若点A(1,2)在此图象上,则不等式kx+b>2的解集为( )| A. | x>1 | B. | x<1 | C. | x>0 | D. | x<0 |
20.(-0.7)2的平方根是( )
| A. | -0.7 | B. | 0.7 | C. | ±0.7 | D. | 0.49 |
17. 在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是$\sqrt{2}$和-1,则点C所对应的实数是( )
在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是$\sqrt{2}$和-1,则点C所对应的实数是( )
 在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是$\sqrt{2}$和-1,则点C所对应的实数是( )
在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是$\sqrt{2}$和-1,则点C所对应的实数是( )| A. | 1+$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 2$\sqrt{2}$-1 | D. | 2$\sqrt{2}$+1 |

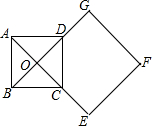 如图,正方形ABCD的对角线相交于点O,正方形OEFG的一边OG经过点D,且D是OG的中点,OG=$\sqrt{2}$AB,若正方形ABCD固定,将正方形OEFG绕O点逆时针旋转α角,(0°<α<360°)得到正方形OE′F′G′,当α=30或150度时,∠OAG′=90°.
如图,正方形ABCD的对角线相交于点O,正方形OEFG的一边OG经过点D,且D是OG的中点,OG=$\sqrt{2}$AB,若正方形ABCD固定,将正方形OEFG绕O点逆时针旋转α角,(0°<α<360°)得到正方形OE′F′G′,当α=30或150度时,∠OAG′=90°. 如图,将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE,BC的延长线交DE于F,连接BD,若BC=2EF,试证明△BED是等腰三角形.
如图,将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE,BC的延长线交DE于F,连接BD,若BC=2EF,试证明△BED是等腰三角形.